
| A. | 2$\sqrt{3}$-2 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{3}$+1 | D. | 2$\sqrt{3}$+2 |
分析 根据点P为双曲线上一点,且∠PF1F2=30°,∠PF2F1=60°,可得|PF1|=$\sqrt{3}$c,|PF2|=c,利用双曲线的定义,可求双曲线的离心率.
解答 解:设双曲线的焦距长为2c,
∵点P为双曲线上一点,且∠PF1F2=30°,∠PF2F1=60°,
∴P在右支上,∠F2PF1=90°,
即PF1⊥PF2,|PF1|=2csin60°=$\sqrt{3}$c,|PF2|=2ccos60°=c,
∴由双曲线的定义可得|PF1|-|PF2|=($\sqrt{3}$-1)c=2a,
∴e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1.
故选:C.
点评 本题考查双曲线的定义、方程和性质,解题的关键是确定|PF1|=$\sqrt{3}$c,|PF2|=c,运用定义法和离心率公式,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
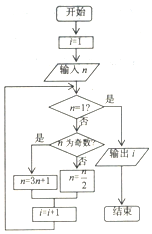 20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )
20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )| A. | 5 | B. | 16 | C. | 5或32 | D. | 4或5或32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{{\sqrt{3}}}{3},\frac{{4\sqrt{3}}}{11}}]$ | B. | $({\frac{{\sqrt{3}}}{9},\frac{{\sqrt{3}}}{3}})$ | C. | $({\frac{{\sqrt{3}}}{9},\frac{{4\sqrt{3}}}{11}}]$ | D. | $({\frac{{\sqrt{3}}}{9},\frac{{2\sqrt{3}}}{11}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com