
分析 由对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),得到f(x1)max<g(x2)max.由此能求出结果.
解答 解:∵函数f(x)=lnx+ax和g(x)=x2-2x+2,
若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),
∴f(x1)max<g(x2)max.
∵f′(x)=$\frac{1}{x}$+a,x1∈(0,+∞),
由f′(x)=0,得x=-$\frac{1}{a}$.
∴f(x1)max=f(-$\frac{1}{a}$)=ln(-$\frac{1}{a}$)-1.
∵g′(x)=2x-2,x2∈[0,1],
∴g′(x2)<0,∴g(x2)max=g(0)=0-2×0+2=2.
∴由f(x1)max<g(x2)max,得ln(-$\frac{1}{a}$)-1<2,
∴ln(-$\frac{1}{a}$)<lne3,
解得a<-$\frac{1}{{e}^{3}}$.
故答案为:(-∞,-$\frac{1}{{e}^{3}}$).
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数的性质的合理运用.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
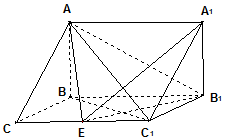 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
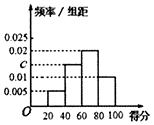 某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不合格 | 合格 | ||
| 得分 | [20,40) | [40,60) | [60,80) | [80,100] |
| 频数 | 6 | a | 24 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$-2 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{3}$+1 | D. | 2$\sqrt{3}$+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com