
【题目】2018年“双十一”期间,某商场举办了一次有奖促销活动,顾客消费每满1000元可参加一次抽奖(例如:顾客甲消费930元,不得参与抽奖;顾客乙消费3400元,可以抽奖三次)。如图1,在圆盘上绘制了标有A,B,C,D的八个扇形区域,每次抽奖时由顾客按动按钮使指针旋转一次,旋转结束时指针会随机停在圆盘上的某一个位置,顾客获奖的奖次由指针所指区域决定(指针与区域边界线粗细忽略不计)。商家规定:指针停在标A,B,C,D的扇形区域分别对应的奖金为200元、150元、100元和50元。已知标有A,B,C,D的扇形区域的圆心角成等差数列,且标D的扇形区域的圆心角是标A的扇形区域的圆心角的4倍.

(I)某顾客只抽奖一次,设该顾客抽奖所获得的奖金数为X元,求X的分布列和数学期望;
(II)如图2,该商场统计了活动期间一天的顾客消费情况.现按照消费金额分层抽样选出15位顾客代表,其中获得奖金总数不足100元的顾客代表有7位.现从这7位顾客代表中随机选取两位,求这两位顾客的奖金总数和仍不足100元的概率.
【答案】(1)详见解析(2)![]()
【解析】
(1)分别计算出X=50,100,150,200对应的概率,计算期望,即可。(2)结合古典概型,计算出![]() ,结合
,结合![]() ,即可。
,即可。
解:(1)设标有A,B,C,D的扇形区域的圆心角分别为![]()
由题意知:![]()
所以顾客抽奖一次,获得奖金X可能取值为50,100,150,200,所对应的概率分别为 ![]()
所以X的分布列为
X | 50 | 100 | 150 | 200 |
P |
|
|
|
|
期望![]()
(2)由已知得:
1消费金额位于![]() 内的顾客,获奖金额一定高于100元,
内的顾客,获奖金额一定高于100元,
2消费金额位于![]() 内的顾客获奖金额为0元,
内的顾客获奖金额为0元,
3消费金额位于![]() 内的顾客获奖金额可能为50,100,150,200元
内的顾客获奖金额可能为50,100,150,200元
分层抽样得 ![]() 内抽到的顾客代表人数为
内抽到的顾客代表人数为![]() 人,
人,
则获得奖金总数不足100元的剩余4位顾客代表必然获得奖金数为50元.
设获奖金额为0元的三位顾客代表为![]() ,获奖金额为50元的四位顾客代表为
,获奖金额为50元的四位顾客代表为 ![]()
事件 ![]() “从这7位顾客代表中随机选取两位的奖金总数仍不足100元”
“从这7位顾客代表中随机选取两位的奖金总数仍不足100元”
![]() “从这7位顾客代表中随机选取两位的奖金总数等于100元”
“从这7位顾客代表中随机选取两位的奖金总数等于100元”
从这7位顾客代表中随机选取两位的基本事件空间为:
![]() 共有21个基本事件;
共有21个基本事件;
![]() 共有6个基本事件。
共有6个基本事件。
![]()
从这7位顾客代表中随机选取两位,他们的奖金总数仍不足100元的概率为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号,某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式: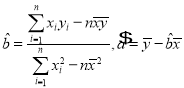 ;参考数据:
;参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
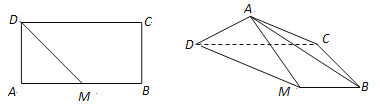
【题目】如图,在矩形ABCD中,AB=2,AD=1,M为AB的中点,将△ADM沿DM翻折.在翻折过程中,当二面角A—BC—D的平面角最大时,其正切值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水果的价格会受到需求量和天气的影响.某采购员定期向某批发商购进某种水果,每箱水果的价格会在当日市场价的基础上进行优惠,购买量越大优惠幅度越大,采购员通过对以往的10组数据进行研究,发现可采用![]() 来作为价格的优惠部分
来作为价格的优惠部分![]() (单位:元/箱)与购买量
(单位:元/箱)与购买量![]() (单位:箱)之间的回归方程,整理相关数据得到下表(表中
(单位:箱)之间的回归方程,整理相关数据得到下表(表中![]() ):
):
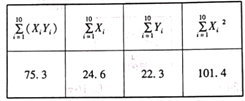
(1)根据参考数据,
①建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②若当日该种水果的市场价为200元/箱,估算购买100箱该种水果所需的金额(精确到0.1元).
(2)在样本中任取一点,若它在回归曲线上或上方,则称该点为高效点.已知这10个样本点中,高效点有4个,现从这10个点中任取3个点,设取到高效点的个数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为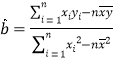 ,
,![]() ,参考数据:
,参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是平面内凸三十五边形的35个顶点,且
是平面内凸三十五边形的35个顶点,且![]() 中任何两点之间的距离不小于
中任何两点之间的距离不小于![]() . 证明:从这35个点中可以选出五个点,使得这五个点中任意两点之间的距离不小于3.
. 证明:从这35个点中可以选出五个点,使得这五个点中任意两点之间的距离不小于3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行某种游戏比赛,规定:每一次胜者得1分,负者得0分;当其中一人的得分比另一人的得分多2分时即赢得这场游戏,比赛随之结束.同时规定:比赛次数最多不超过20次,即经20次比赛,得分多者赢得这场游戏,得分相等为和局.已知每次比赛甲获胜的概率为可![]() ,乙获胜的概率为
,乙获胜的概率为![]() .假定各次比赛的结果是相互独立的,比赛经
.假定各次比赛的结果是相互独立的,比赛经![]() 次结束.求
次结束.求![]() 的期望
的期望![]() 的变化范围.
的变化范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,右顶点为(1,0).
x,右顶点为(1,0).
(1)求双曲线C的方程;
(2)已知直线y=x+m与双曲线C交于不同的两点A,B,且线段AB的中点为![]() ,当x0≠0时,求
,当x0≠0时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com