
【题目】如图,在棱长为2的正方体![]() 中,点
中,点![]() 分别是棱
分别是棱![]() 上的动点,且
上的动点,且![]() .
.
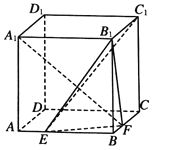
(1)求证:![]() ;
;
(2)当三棱锥![]() 的体积取得最大值时,求二面角
的体积取得最大值时,求二面角![]() 的正切值.
的正切值.
【答案】(1)见证明;(2)![]()
【解析】
设AE=BF=x.以D为原点建立空间直角坐标系,求出相关点的坐标
(1)通过计算![]() ,证明A1F⊥C1E.
,证明A1F⊥C1E.
(2)判断当S△BEF取得最大值时,三棱锥B1﹣BEF的体积取得最大值.求出平面B1EF的法向量,底面ABCD的法向量,设二面角B1﹣EF﹣B的平面角为θ,利用空间向量的数量积求出![]() ,然后求解二面角B1﹣EF﹣B的正切值.
,然后求解二面角B1﹣EF﹣B的正切值.
设AE=BF=x.以D为原点建立空间直角坐标系,得下列坐标:D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),D1(0,0,2),A1(2,0,2),B1(2,2,2),C1(0,2,2),E(2,x,0),F(2﹣x,2,0).
(1)因为![]() ,
,![]() ,
,
所以![]() .
.
所以A1F⊥C1E.

(2)因为![]() ,
,
所以当S△BEF取得最大值时,三棱锥B1﹣BEF的体积取得最大值.
因为![]() ,
,
所以当x=1时,即E,F分别是棱AB,BC的中点时,三棱锥B1﹣BEF的体积取得最大值,此时E,F坐标分别为E(2,1,0),F(1,2,0).
设平面B1EF的法向量为![]() ,
,
则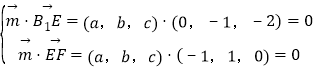 得
得![]()
取a=2,b=2,c=﹣1,得![]() .显然底面ABCD的法向量为
.显然底面ABCD的法向量为![]() .
.
设二面角B1﹣EF﹣B的平面角为θ,由题意知θ为锐角.
因为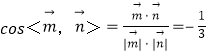 ,所以
,所以![]() ,于是
,于是![]() .
.
所以![]() ,即二面角B1﹣EF﹣B的正切值为
,即二面角B1﹣EF﹣B的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】三角形ABC中,![]() ,AC=1,以B为直角顶点作等腰直角三角形BCD(A、D在BC两侧),当∠BAC变化时,线段AD的长度最大值为._______________.
,AC=1,以B为直角顶点作等腰直角三角形BCD(A、D在BC两侧),当∠BAC变化时,线段AD的长度最大值为._______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为抛物线
为抛物线![]() 外一点,过点
外一点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() .
.

(Ⅰ)若点![]() 为
为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 为圆
为圆![]() 上的点,记两切线
上的点,记两切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系中,点![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 在曲线
在曲线![]() 上运动,以极点为坐标原点,极轴为
上运动,以极点为坐标原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为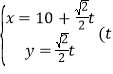 为参数
为参数![]() 。
。
(1)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(2)求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值。
的距离的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年“双十一”期间,某商场举办了一次有奖促销活动,顾客消费每满1000元可参加一次抽奖(例如:顾客甲消费930元,不得参与抽奖;顾客乙消费3400元,可以抽奖三次)。如图1,在圆盘上绘制了标有A,B,C,D的八个扇形区域,每次抽奖时由顾客按动按钮使指针旋转一次,旋转结束时指针会随机停在圆盘上的某一个位置,顾客获奖的奖次由指针所指区域决定(指针与区域边界线粗细忽略不计)。商家规定:指针停在标A,B,C,D的扇形区域分别对应的奖金为200元、150元、100元和50元。已知标有A,B,C,D的扇形区域的圆心角成等差数列,且标D的扇形区域的圆心角是标A的扇形区域的圆心角的4倍.

(I)某顾客只抽奖一次,设该顾客抽奖所获得的奖金数为X元,求X的分布列和数学期望;
(II)如图2,该商场统计了活动期间一天的顾客消费情况.现按照消费金额分层抽样选出15位顾客代表,其中获得奖金总数不足100元的顾客代表有7位.现从这7位顾客代表中随机选取两位,求这两位顾客的奖金总数和仍不足100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
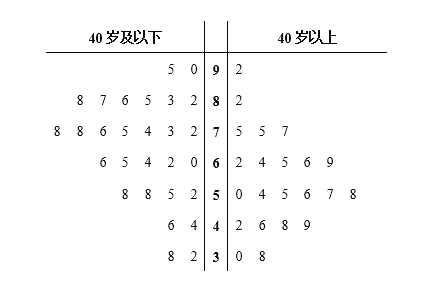
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: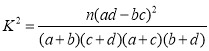 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)![]() 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求![]() 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数).
为这三个数的中位数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,已知椭圆 C:![]() 的离心率为
的离心率为![]() ,且过点 (
,且过点 (![]() ,
,![]() ),点 P 在第四象限, A 为左顶点, B 为上顶点, PA 交 y 轴于点 C,PB 交 x 轴于点 D.
),点 P 在第四象限, A 为左顶点, B 为上顶点, PA 交 y 轴于点 C,PB 交 x 轴于点 D.

(1) 求椭圆 C 的标准方程;
(2) 求 △PCD 面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有学生500人,学校为了解学生的课外阅读时间,从中随机抽取了50名学生,获得了他们某一个月课外阅读时间的数据(单位:小时),将数据分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],整理得到如图所示的频率分布直方图.
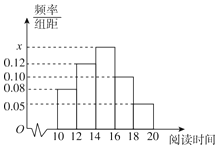
(1)求频率分布直方图中的x的值;
(2)试估计该校所有学生中,课外阅读时间不小于16小时的学生人数;
(3)已知课外阅读时间在[10,12)的样本学生中有3名女生,现从阅读时间在[10,12)的样本学生中随机抽取3人,记X为抽到女生的人数,求X的分布列与数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com