
分析 设该船的位置是从B到A,两个灯塔位置分别为C、D,如图所示.根据题意,得到△ACD中∠CAD=15°,
∠CDA=30°,CD=6,在Rt△ABC中利用三角函数的定义算出AB=10海里,即可得到该船的时速.
解答 解:如图可知∠CDA=30°,CD=6,∠CAB=45°
∴AB=BC=x,
在三角形ABD中tan∠CDA=$\frac{AB}{BD}$=$\frac{x}{x+6}$=$\frac{\sqrt{3}}{3}$,
x=3+3$\sqrt{3}$,
AD=3+3$\sqrt{3}$,
∴这船的航速为3+3$\sqrt{3}$(海里/小时).
点评 本题给出实际应用问题,求轮船的航行时速.着重考查了解直角三角形和方位角等概念,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 8 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 14种 | C. | 16种 | D. | 18种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
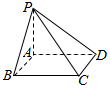 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AB=1,当直线PD与平面PBC所成角的正弦值最大时,该几何体的外接球的体积为$\frac{\sqrt{3}π}{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AB=1,当直线PD与平面PBC所成角的正弦值最大时,该几何体的外接球的体积为$\frac{\sqrt{3}π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0,且x≠-1} | B. | {x|x<0} | C. | {x|x<-1} | D. | {x|x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期变为原来的3倍,纵坐标不变 | |
| B. | 周期变为原来的$\frac{1}{3}$,纵坐标不变 | |
| C. | 纵坐标伸长为原来的3倍,周期不变 | |
| D. | 纵坐标伸长为原来的$\frac{1}{3}$倍,周期不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com