
(本小题满分13分)为抗击金融风暴,某工贸系统决定对所属企业给予低息贷款的扶持,该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表:
| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
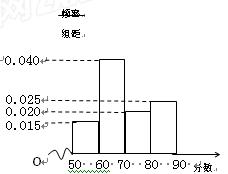
解:(1)因为0.015×10="0.15, " 0.04×10=0.4,在频率分布直方图中,中位数左边和右边的面积相等,所以中位数在区间[60,70)内,
设中位数为x,则(60-50)×0.015+(x-60)×0.04=0.5,解得x=68.75
所以估计该系统所属企业评估得分的中位数是68.75. ………………2分
平均分为:55×0.15+65×0.4+75×0.2+85×0.25=70.5分. ………………4分
………………4分
(2)依题意,整改后优秀企业的频率为10×0.025=0.25, ………5分
不合格企业,合格企业,良好企业的频率成等差数列,设该等差数列的首项为a,公差为d,则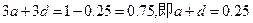 ………………7分
………………7分
设该系统所属企业获得贷款的均值为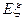 ,则
,则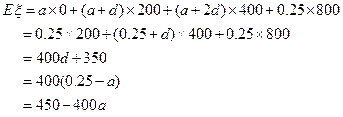 ………………10分
………………10分
由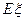 ≥410,得450
≥410,得450 -400a≥410,即a≤0.1.
-400a≥410,即a≤0.1.  ………………12分
………………12分
故整改后不合格企业占企业总数的百分比的 最大值是10%. ………………13分
最大值是10%. ………………13分
解析


科目:高中数学 来源: 题型:解答题
甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
| 甲 | 8 | 6 | 7 | 8 | 6 | 5 | 9 | 10 | 4 | 7 |
| 乙 | 6 | 7 | 7 | 8 | 6 | 7 | 8 | 7 | 9 | 5 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为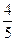 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为 ,
, (
( >
> ),且不同种产品是否受欢迎相互独立。记
),且不同种产品是否受欢迎相互独立。记 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
 | 0 | 1 | 2 | 3 |
 |  |  |  |  |
 ,
, 的值;
的值; 。
。查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下表的统计资料:
若由资料可知y对x呈线性相关关系,试求:
(1)线性回归直线方程;
(2)估计使用年限为.10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分).
某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段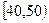 ,
,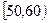 ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)求分数在 内的频率;
内的频率;
(2)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.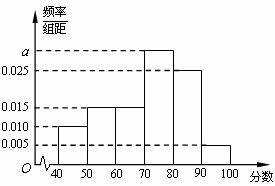
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
育新中学的高二一班男同学有45名,女同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.
(1)求被抽到的课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名中恰有一名女同学的概率;
(3)试验结束后,第一次做试验的同学得到的试验数据为68,70,71,72,74,第二次做试验的同学得到的试验数据为69,70,70,72,74,请问哪位同学的实验更稳定?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
、某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天100颗种子的发芽数,如下
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数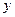 颗 颗 | 23 | 25 | 30 | 26 | 16 |
 求线性回归方程,再用被选取点2组数据进行检验
求线性回归方程,再用被选取点2组数据进行检验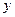 关于
关于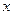 的线性回归方程
的线性回归方程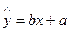 ;
;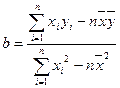 ,
,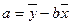
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某校举行的数学知识竞赛中,将参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右 依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.
依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.
(1)求成绩在50—70分的频率是多少;
(2)求这次参赛学生的总人数是多少;
(3)求这次数学竞赛成绩的平均分的近似值.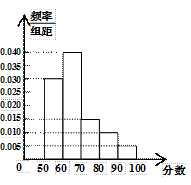
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
17.有甲乙两个班级进行数学考 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10[来源:学科网ZXXK] | | |
| 乙班 | | 30 | [来源:学#科#网] |
| 合计 | | | 105 |
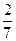
 绩与班级有关系”。
绩与班级有关系”。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com