
甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
| 甲 | 8 | 6 | 7 | 8 | 6 | 5 | 9 | 10 | 4 | 7 |
| 乙 | 6 | 7 | 7 | 8 | 6 | 7 | 8 | 7 | 9 | 5 |

科目:高中数学 来源: 题型:解答题
(本小题满分12分)
PM2. 5是指大气中直径小于或等于2. 5微米的颗粒物,也称为 可人肺颗粒物.我国PM2. 5标准采用世卫组织设定的最宽限 值,即PM2.5日均值在35微克/立方米以下空气质量为一级; 在35微克/立方米~75微克/立方米之间空气质量为二级;在 75微克/立方米以上空气质量为超标.
某市环保局从市区2012年全年每天的PM2.5监测数据中 随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为 茎,个位为叶)
(I)从这9天的数据中任取2天的数据,求恰有一天空气质量达到一级的概率;
(II) 以这9天的PM2. 5日均值来估计供暖期间的空气质量情况,则供暖期间(按150天计算)中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(10分)某种产品的广告费支出x与消费额y(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
 关于
关于 的线性回归方程
的线性回归方程 ;
; ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了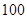 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| | 数学 | 语文 | 总计 |
| 初中 | 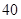 | 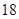 | 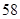 |
| 高中 | 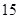 | 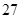 | 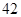 |
| 总计 | 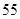 | 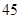 | 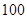 |
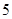 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?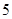 名学生中任取
名学生中任取 名,求恰有
名,求恰有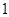 名初中学生的概率.
名初中学生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现在采用分层抽样法(层内采用不放回的简单随机抽样)从甲,乙两组中共抽取3人进行技术考核.
(1)求甲,乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工的概率;
(3)令X表示抽取的3名工人中男工人的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某种产品的广告费支出 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
 关于
关于 的线性回归方程
的线性回归方程 .(其中
.(其中 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
| 甲 | 82 | 82 | 79 | 95 | 87 |
| 乙 | 95 | 75 | 80 | 90 | 85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
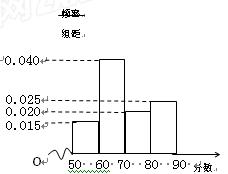
(本小题满分13分)为抗击金融风暴,某工贸系统决定对所属企业给予低息贷款的扶持,该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表:
| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com