
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性求得ω的值.
(2)根据f(x)的解析式,利用正弦函数的单调性,求得f(x)的单调区间.
解答 解:(1)∵函数f(x)=2sin(ωx-$\frac{5π}{6}$)+2$\sqrt{3}$sinωx=2sinωx•(-$\frac{\sqrt{3}}{2}$)-2cosωx•$\frac{1}{2}$+2$\sqrt{3}$sinωx
=$\sqrt{3}$sinωx-cosωx=2sin(ωx-$\frac{π}{6}$) 的最小正周期T=|$\frac{2π}{ω}$|=π,∴ω=±2.
(2)①当ω=2时,f(x)=2sin(2x-$\frac{π}{6}$),令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2x+$\frac{π}{2}$,求得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,
可得函数的增区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.
同理,令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2x+$\frac{3π}{2}$,求得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,可得函数的减区间为[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],k∈Z.
②当ω=-2,f(x)=2sin(-2x-$\frac{π}{6}$)=-2sin(2x+$\frac{π}{6}$),令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2x+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,
可得函数的减区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
同理,令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2x+$\frac{3π}{2}$,求得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,可得函数的增区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
点评 本题主要考查三角恒等变换,正弦函数的周期性、单调性,属于中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
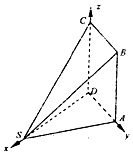 如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,$SD=\sqrt{3}AD$.
如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,$SD=\sqrt{3}AD$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③ | C. | ①② | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
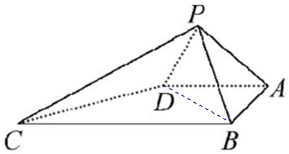 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90℃,BC=2AD,△PAB与△PAD都是等边三角形,平面ABCD⊥平面PBD.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90℃,BC=2AD,△PAB与△PAD都是等边三角形,平面ABCD⊥平面PBD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a≥\frac{1}{3}$ | B. | $a≤-\frac{1}{3}$ | C. | $-\frac{1}{3}≤a≤\frac{1}{3}$ | D. | $a≥\frac{1}{3}$或$a≤-\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com