Question

20．向一等边三角形内随机撒1000个点，则落在该等边三角形内切圆的点约有（　　）

• A． 850个
• B． 605个
• C． 415个
• D． 295个

Answer 1

分析 求出三角形的面积，再求出内切圆的面积，根据几何概型概率计算公式，求其比值即可解答．

解答 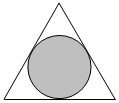解：不妨设三角形边长为1，则三角形面积为$\frac{\sqrt{3}}{4}$，
内切圆的半径为等边三角形高的三分之一，
即$\frac{1}{3}×\frac{1}{2}×\sqrt{3}$=$\frac{\sqrt{3}}{6}$，
∴内切圆面积为$π×（\frac{\sqrt{3}}{6}）^{2}$=$\frac{1}{12}$π，
则点M落在其内切圆内部（阴影）区域的概率为$\frac{\frac{π}{12}}{\frac{\sqrt{3}}{4}}$=$\frac{\sqrt{3}π}{9}$，
∵向一等边三角形内随机撒1000个点，
∴落在该等边三角形内切圆的点约有1000×$\frac{\sqrt{3}π}{9}$≈605个．
故选D．

点评 本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．