练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．底面为正方形，顶点在底面的投影为底面中心的棱锥P-ABCD的五个顶点在同一球面上，若该棱锥的底面边长为4，侧棱长为2$\sqrt{6}$，则这个球的表面积为36π．

    分析 画出图形，正四棱锥P-ABCD的外接球的球心在它的高PO1上，记为O，求出PO1，OO1，解出球的半径，求出球的表面积．

    解答 解：正四棱锥P-ABCD的外接球的球心在它的高PO1上，
    记为O，PO=AO=R，PO1=4，OO1=R-4，或OO1=4-R（此时O在PO1的延长线上），
    在Rt△AO1O中，R2=8+（R-4）2得R=3，∴球的表面积S=36π
    故答案为：36π．

    点评 本题考查球的表面积，球的内接体问题，考查计算能力，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．某情报站有A，B，C，D四种互不相同的密码，每周使用其中的一种密码，且每周都是从上周未使用的三种密码中等可能地随机选用一种．设第1周使用A种密码，那么第5周也使用A种密码的概率是（　　）
    A．$\frac{7}{27}$B．$\frac{8}{27}$C．$\frac{10}{27}$D．$\frac{11}{27}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=$\frac{x+m}{x+1}$，且存在函数s=φ（t）=at+b（t＞$\frac{1}{2}$，a≠0），满足f（$\frac{2t-1}{t}$）=$\frac{2s+1}{s}$．
    （1）求m的值；
    （2）证明：存在函数t=φ（s）=cs+d（s＞0），满足f（$\frac{2s+1}{s}$）=$\frac{2t-1}{t}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

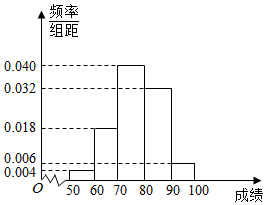    3．到2016年，北京市高考英语总分将由150分降低到100分，语文分值将相应增加．某校高三学生率先尝试100分制英语考试，从中随机抽出50人的英语成绩作为样本并进行统计，将测试结果按如下方式分成五组：第一组[50，60]，第二组[60，70]，…第五组[90，100]，如图是按上述分组方法得到的频率分布直方图．
    （1）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计这次参加英语考试的高三学生的英语平均成绩；
    （2）从这五组中抽取14人进行座谈，若抽取的这14人中，恰好有2人成绩为50分，7人成绩为70分，2人成绩为75分，3人成绩为80分，求这14人英语成绩的方差；
    （3）从50人的样本中，随机抽取测试成绩在[50，60]∪[90，100]内的两名学生，设其测试成绩分别为m，n
    （i）求事件“|m-n|＞30”的概率；
    （ii）求事件“mn≤3600”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．一盒中有形状，大小相同的6张刮奖券，其中一等奖1张，二等奖2张，三等奖3张，某人从中一次性随机摸出2张，则中不同的奖项的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{2}{5}$C．$\frac{4}{5}$D．$\frac{11}{15}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．向一等边三角形内随机撒1000个点，则落在该等边三角形内切圆的点约有（　　）
    A．850个B．605个C．415个D．295个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知△ABC的三个顶点A（-1，0），B（1，0），C（2，3），其外接圆为圆H．
    （Ⅰ）求圆H的方程；
    （Ⅱ）若直线l过点C，且被圆H截得的弦长为2，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．气修专业共录取了81名学生，现准备分成两个班，其中一个班40人，二班41人，则不同的分法有（　　）
    A．P${\;}_{81}^{40}$种B．C${\;}_{81}^{40}$种
    C．C${\;}_{81}^{40}$+C${\;}_{41}^{41}$种D．C${\;}_{81}^{40}$C${\;}_{81}^{41}$种

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某校高二八班选出甲、乙、丙三名同学参加级部组织的科学知识竞赛．在该次竞赛中只设成绩优秀和成绩良好两个等次，若某同学成绩优秀，则给予班级10分的班级积分，若成绩良好，则给予班级5分的班级积分．假设甲、乙、丙成绩为优秀的概率分别为$\frac{2}{3}$，$\frac{1}{2}$，$\frac{1}{3}$，他们的竞赛成绩相互独立．
    （1）求在该次竞赛中甲、乙、丙三名同学中至少有一名成绩为优秀的概率；
    （2）记在该次竞赛中甲、乙、丙三名同学所得的班级积分之和为随机变量ξ，求随机变量ξ的分布列和数学期望Eξ．

    查看答案和解析>>

    同步练习册答案