
分析 函数f(x)是定义在R 上的奇函数,且当x<0时,f(x)=x-x2,可得出函数在R上是增函数,由此性质转化求解不等式,解出参数范围即可.
解答 解:函数f(x)当x<0时,f(x)=x-x2,由二次函数的性质知,它在(-∞,0)上是增函数,
又函数f(x)是定义在R 上的奇函数,
故函数f(x)是定义在R 上的增函数,
∵f(m)+f(m-2)>0,可得f(m)>-f(m-2)=f(2-m)
∴m>2-m,解得:1<m,
实数m 的取值范围是(1,+∞)
故答案为:(1,+∞).
点评 本题考查奇偶性与单调性的综合,求解本题关键是根据函数的奇偶性与单调性得出函数在R上的单调性,利用单调性将不等式f(m)+f(m-2)>0转化为代数不等式,求出实数m 的取值范围,本题是奇偶性与单调性结合的一类最主要的题型.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
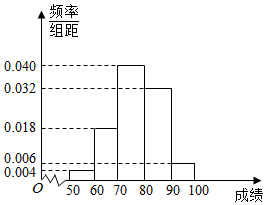 到2016年,北京市高考英语总分将由150分降低到100分,语文分值将相应增加.某校高三学生率先尝试100分制英语考试,从中随机抽出50人的英语成绩作为样本并进行统计,将测试结果按如下方式分成五组:第一组[50,60],第二组[60,70],…第五组[90,100],如图是按上述分组方法得到的频率分布直方图.
到2016年,北京市高考英语总分将由150分降低到100分,语文分值将相应增加.某校高三学生率先尝试100分制英语考试,从中随机抽出50人的英语成绩作为样本并进行统计,将测试结果按如下方式分成五组:第一组[50,60],第二组[60,70],…第五组[90,100],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P${\;}_{81}^{40}$种 | B. | C${\;}_{81}^{40}$种 | ||
| C. | C${\;}_{81}^{40}$+C${\;}_{41}^{41}$种 | D. | C${\;}_{81}^{40}$C${\;}_{81}^{41}$种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
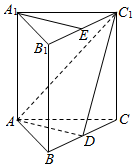 如图,在三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在三棱柱ABC-A1B1C1中,D是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com