Question

2．已知函数f（x）=|2x+1|．
（Ⅰ）用分段函数的形式表示该函数；
（Ⅱ）在如图所给的坐标系中画出该函数的图象；并根据图象直接写出该函数的定义域、值域、单调区间（不要求证明）

Answer 1

分析 （Ⅰ）利用零点分段，即可用分段函数的形式表示该函数；
（Ⅱ）根据（Ⅰ）中函数的图象，我们可以分析出自变量，函数值的取值范围，从而得到定义域和值域，分析出从左到右函数图象上升和下降的区间，即可得到函数的单调区间．

解答 解：（Ⅰ）$f（x）=\left\{\begin{array}{l}2x+1，x≥-\frac{1}{2}\\-2x-1，x＜-\frac{1}{2}\end{array}\right.$…（4分）
（Ⅱ）图象如图所示…（6分）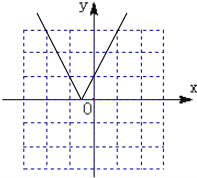

定义域：R，值域：[0，+∞），递增区间：$[-\frac{1}{2}，+∞）$，递减区间：$（-∞，-\frac{1}{2}]$…（12分）

点评 本题考查的知识点是分段函数的解析式求法及其图象的作法，函数的定义域及其求法，函数的值域，函数的图象，其中利用零点分段法求出函数的解析式是解答本题的关键．