
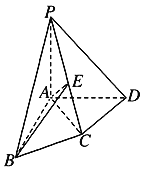
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)关键证明CD⊥平面PAC,(2)关键证明AE⊥PD,AB⊥PD。
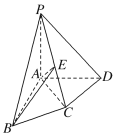
证明:(1)在四棱锥![]() 中,
中,
∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD.∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
而AE平面PAC,∴CD⊥AE.
(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.
∵E是PC的中点,∴AE⊥PC.
由(1)知AE⊥CD,且PC∩CD=C,
∴AE⊥平面PCD.
而PD平面PCD,∴AE⊥PD.
∵PA⊥平面ABCD,∴PA⊥AB.
又∵AB⊥AD且PA∩AD=A,
∴AB⊥平面PAD,而PD平面PAD,
∴AB⊥PD.
又∵AB∩AE=A,
∴PD⊥平面ABE.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】某超市为调查会员某年度上半年的消费情况制作了有奖调查问卷发放给所有会员,并从参与调查的会员中随机抽取![]() 名了解情况并给予物质奖励.调查发现抽取的
名了解情况并给予物质奖励.调查发现抽取的![]() 名会员消费金额(单位:万元)都在区间
名会员消费金额(单位:万元)都在区间![]() 内,调查结果按消费金额分成
内,调查结果按消费金额分成![]() 组,制作成如下的频率分布直方图.
组,制作成如下的频率分布直方图.
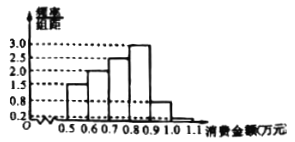
(1)求该![]() 名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
(2)现采用分层抽样的方式从前![]() 组中选取
组中选取![]() 人进行消费爱好调查,然后再从前
人进行消费爱好调查,然后再从前![]() 组选取的人中随机选
组选取的人中随机选![]() 人,求这
人,求这![]() 人都来自第
人都来自第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )

A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在坐标原点,焦点在
中心在坐标原点,焦点在![]() 轴上,且过
轴上,且过![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 两点不是左右顶点),若直线
两点不是左右顶点),若直线![]() 的斜率为
的斜率为![]() 时,弦
时,弦![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若以![]() ,
,![]() 两点为直径的圆过椭圆的右顶点,则直线
两点为直径的圆过椭圆的右顶点,则直线![]() 是否经过定点,若是,求出定点坐标,若不是,请说明理由.
是否经过定点,若是,求出定点坐标,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com