
分析 根据题意,分析可得该女子每天织布的量组成了等比数列{an},且其公比q=2,又由她5天共织布5尺,可得S5=$\frac{{a}_{1}(1-{2}^{5})}{1-2}$=5,解可得a1的值,结合题意,可得Sn=$\frac{{a}_{1}(1-{2}^{n})}{1-2}$≥20,解可得n的范围,即可得答案.
解答 解:由题意可得:该女子每天织布的量组成了等比数列{an},且其公比q=2,
若她5天共织布5尺,即S5=5,则$\frac{{a}_{1}(1-{2}^{5})}{1-2}$=5,解可得a1=$\frac{5}{31}$,
若Sn≥20,则有$\frac{{a}_{1}(1-{2}^{n})}{1-2}$≥20,即2n≥125
解可得n≥7,
即若要使织布的总尺数不少于20尺,该女子所需7天;
故答案为:7.
点评 本题考查等比数列的前n项和性质,关键是分析题意,将原问题转化为等比数列前n项和问题.


科目:高中数学 来源: 题型:选择题

| A. | 8$\sqrt{2}$+2$\sqrt{5}$+6,8 | B. | 2$\sqrt{2}$+8$\sqrt{5}$+6,8 | C. | 4$\sqrt{2}$+8$\sqrt{5}$+12,16 | D. | 8$\sqrt{2}$+4$\sqrt{5}$+12,16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=2,φ=$\frac{π}{2}$ | B. | ω=$\frac{1}{2}$,φ=$\frac{π}{2}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{4}$ | D. | ω=2,φ=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | ($\frac{2\sqrt{3}}{3}$,2) | C. | [$\frac{2\sqrt{3}}{3}$,2] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
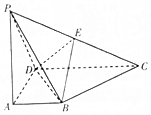 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | 1009 | C. | 2017 | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,-1) | B. | (2,4] | C. | [-4,-1)∪(2,4] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2017n-m | B. | n-2017m | C. | m | D. | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com