
分析 (1)若m=-1,化简集合,即可求A∩∁RB;
(2)若A∪B=A,B⊆A,利用集合关系即可求实数m的取值范围.
解答 解:(1)若m=-1,则B={x|-3<x<0},
所以CRB={x|x≤-3或x≥0},(2分)
又A={x|(x-4)(x+3)≤0}={x|-3≤x≤4},(4分)
所以A∩CRB={x|0≤x≤4或x=-3};(5分)
(2)因为A∪B=A所以B⊆A,(6分)
当B=Φ时,显然B⊆A,
此时2m-1≥m+1解得m≥2;(8分)
当B≠Φ时,则由B⊆A得-3≤2m-1<m+1≤4,
解得-1≤m<2;(11分)
综合上述,实数m的取值范围为m≥-1.(12分)
点评 本题主要考查集合的基本运算,根据集合关系建立不等式关系是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
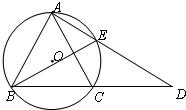 如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com