练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为践行“绿水青山就是金山银山”的发展理念和提高生态环境的保护意识，高二年级准备成立一个环境保护兴趣小组.该年级理科班有男生400人，女生200人；文科班有男生100人，女生300人.现按男、女用分层抽样从理科生中抽取6人，按男、女分层抽样从文科生中抽取4人，组成环境保护兴趣小组，再从这10人的兴趣小组中抽出4人参加学校的环保知识竞赛.

    （1）设事件为“选出的这4个人中要求有两个男生两个女生，而且这两个男生必须文、理科生都有”，求事件发生的概率；

    （2）用表示抽取的4人中文科女生的人数，求的分布列和数学期望.

    【答案】（1）；（2）见解析

    【解析】

    （1）按分层抽样得抽取了理科男生4人，女生2人，文科男生1人，女生3人，再利用古典概型求解即可（2）由超几何分布求解即可

    （1）因为学生总数为1000人，该年级分文、理科按男女用分层抽样抽取10人，则抽取了理科男生4人，女生2人，文科男生1人，女生3人.

    所以.

    （2）的可能取值为0,1,2,3，

    ，

    ，

    ，

    ，

    的分布列为

    0

    1

    2

    3

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知是函数的切线，则的最小值为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C1：x2+y2=1与圆C2：x2+y2﹣6x+m=0．

    （1）若圆C1与圆C2外切，求实数m的值；

    （2）在（1）的条件下，若直线x+2y+n=0与圆C2的相交弦长为2，求实数n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂生产的产品的直径均位于区间内（单位： ).若生产一件产品的直径位于区间内该厂可获利分别为10，30，20，10(单位：元），现从该厂生产的产品中随机抽取200件测量它们的直径，得到如图所示的频率分布直方图.

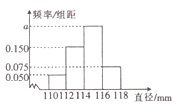
    （1）求的值，并估计该厂生产一件产品的平均利润；

    （2）现用分层抽样法从直径位于区间内的产品中随机抽取一个容量为5的样本，从样本中随机抽取两件产品进行检测，求两件产品中至多有一件产品的直径位于区间内的槪率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其图象关于直线对称，为了得到函数的图象，只需将函数的图象上的所有点（ ）

    A.先向左平移个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变

    B.先向右平移个单位长度，再把所得各点横坐标缩短为原来的，纵坐标保持不变

    C.先向右平移个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变

    D.先向左平移个单位长度，再把所得各点横坐标缩短为原来的，纵坐标保持不变

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示在四棱锥中，下底面为正方形，平面平面，为以为斜边的等腰直角三角形，，若点是线段上的中点.

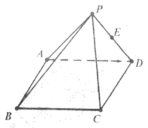
    （1）证明平面.

    （2）求二面角的平面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数（，e是自然对数的底数，）存在唯一的零点，则实数a的取值范围为( )

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ，其中.

    （1）当时，求函数的值域；

    （2）若对任意，均有，求的取值范围；

    （3）当时，设，若的最小值为，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

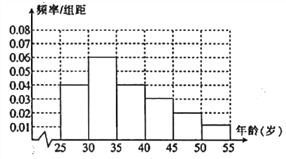
    【题目】某高校进行社会实践，对岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查，开通“微博”的为“时尚族”，否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示，其中在岁， 岁年龄段人数中，“时尚族”人数分别占本组人数的、.

    （1）求岁与岁年龄段“时尚族”的人数；

    （2）从岁和岁年龄段的“时尚族”中，采用分层抽样法抽取6人参加网络时尚达人大赛，其中两人作为领队．求领队的两人年龄都在岁内的概率。

    查看答案和解析>>

    同步练习册答案