
 .
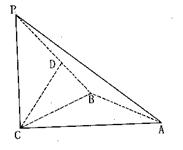
. 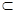 平面ABC,得到PC⊥AB.根据CD⊥平面PAB,AB
平面ABC,得到PC⊥AB.根据CD⊥平面PAB,AB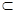 平面PAB,得到OC⊥AB.因此AB平面PCB.
平面PAB,得到OC⊥AB.因此AB平面PCB. 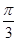 .
. 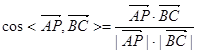

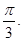
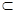 平面ABC,∴PC⊥AB. 2分
平面ABC,∴PC⊥AB. 2分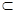 平面PAB,∴OC⊥AB. 3分
平面PAB,∴OC⊥AB. 3分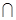 CD=C,∴AB平面PCB. 4分
CD=C,∴AB平面PCB. 4分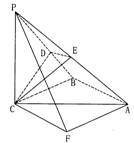
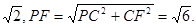
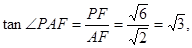
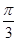 . 12分
. 12分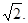
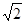 ,0),B(0,0,0),C(
,0),B(0,0,0),C(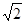 ,0,0),P(
,0,0),P(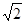 ,0,2).
,0,2).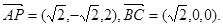 8分
8分
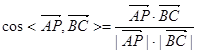

 12分
12分

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:不详 题型:解答题
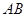 是圆的直径,
是圆的直径,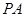 垂直圆所在的平面,
垂直圆所在的平面,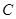 是圆上任一点,
是圆上任一点,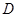 是线段
是线段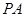 的中点,
的中点,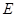 是线段
是线段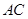 上的一点.
上的一点.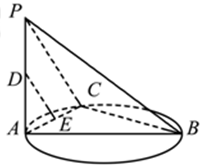
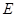 为线段
为线段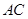 中点,则
中点,则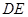 ∥平面
∥平面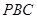 ;
;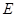 在
在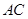 何处,都有
何处,都有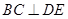 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
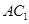 ∥平面
∥平面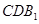 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
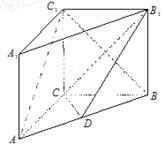
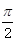 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .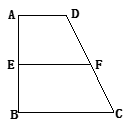
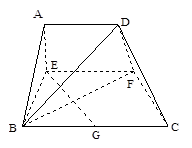
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
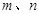 是两条不同的直线,
是两条不同的直线,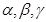 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: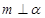 ,
,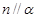 ,则
,则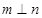
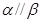 ,
,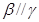 ,
,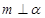 ,则
,则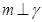
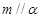 ,
,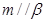 ,
,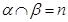 ,则
,则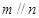
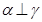 ,
,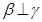 ,
,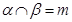 ,则
,则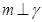
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
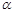 ,
,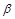 ,
,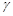 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题: 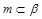 ,
, ,则
,则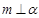 ;
;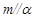 ,
,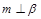 ,则
,则 ;
; ,
,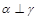 ,则
,则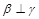 ;
;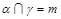 ,
,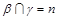 ,
,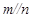 ,则
,则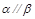 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
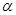 和
和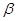 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: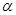 外一条直线
外一条直线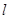 与
与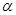 内一条直线平行,则
内一条直线平行,则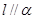 ;
;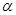 内两条相交直线分别平行于
内两条相交直线分别平行于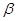 内的两条直线 ,则
内的两条直线 ,则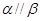 ;
;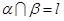 ,若
,若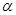 内有一条直线垂直于
内有一条直线垂直于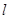 ,则
,则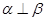 ;
;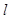 与平面
与平面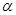 内的无数条直线垂直,则
内的无数条直线垂直,则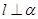 .
.| A.①③ | B.②④ | C.①② | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com