设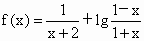
．
(1)试判断函数f(x)的单调性，并给出证明：
(2)解关于x的不等式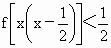
科目：高中数学 来源：北京市海淀区2008－2009学年度高三年级第一学期期中练习数学文科 题型：044
设f(x)是定义在D上的函数，若对D中的任意两数x1，x2(x1≠x2)，恒有
，则称f(x)为定义在D上的C函数．
(1)试判断函数f(x)＝x2是否为定义域上的C函数，并说明理由；
(2)若函数f(x)是R上的奇函数，试证明f(x)不是R上的C函数；
(3)设f(x)是定义在D上的函数，若对任何实数a∈(0，1)以及D中的任意两数x1，x2，恒有f(ax1＋(1－a)x2]≤af(x1)＋(1－a)f(x2)，则称f(x)为定义在D上的C函数．已知f(x)是R上的C函数，m是给定的正整数，设an＝f(n)，n，0，1，2，…，m，且a0=0，am＝2m，记Sf＝a1＋a2＋…＋am对于满足条件的任意函数f(x)，试求Sf的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
设f(x)=log2
,F(x)=
+f(x).
(1)试判断函数f(x)的单调性，并用函数单调性定义，给出证明；
(2)若f(x)的反函数为f－1(x),证明: 对任意的自然数n(n≥3),都有f－1(n)>
;
(3)若F(x)的反函数F－1(x),证明: 方程F－1(x)=0有惟一解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
得－1＜x＜1，
，则
．
，
，
．
，∴f(x)在(－1，1)上是减函数．
．
．
．
．
.