练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

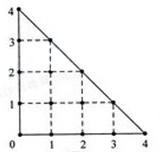
    某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横的交叉点记忆三角形的顶点）处都种了一株相同品种的作物。根据历年的种植经验，一株该种作物的年收获量Y（单位：kg）与它的“相近”作物株数X之间的关系如下表所示：

    X
    		1
    		2
    		3
    		4
    Y
    		51
    		48
    		45
    		42
    这里，两株作物“相近”是指它们之间的直线距离不超过1米。

    （I）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近”的概率；
    （II）从所种作物中随机选取一株，求它的年收获量的分布列与数学期望。

    （I）
    （II）所求分布列为

    X
    		51
    		48
    		45
    		43
    P




    期望

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4.
    (Ⅰ)从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；
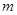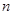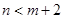    (Ⅱ)先从袋中随机取一个球，该球的编号为，将球放回袋中，然后再从袋中随机取一个球，该球的编号为，求的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    “中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表：

     
    		男性
    		女性
    		合计
    反感
    		10
    		 
    		 
    不反感
    		 
    		8
    		 
    合计
    		 
    		 
    		30
    已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是．
    (Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果，不需要写求解过程)，并据此资料分析反感“中国式过马路 ”与性别是否有关？
    (Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动，记反感“中国式过马路”的人数为X，求X的分布列和数学期望．
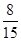    P(K2>k)
    		0.05
    		0.025
    		0.010
    		0.005
    k
    		3.841
    		5.024
    		6.635
    		7.879
    下面的临界值表供参考：
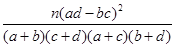    (参考公式：K2=，其中n="a+b+c+d)"

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元.根据历史资料，得到销售季度内市场需求量的频率分布直方图，如右图所示.经销商为下一个销售季度购进了130t该农产品.以x（单位：t，100≤x≤150）表示下一个销售季度内经销该农产品的数量，T表示利润.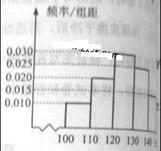

    （Ⅰ）将T表示为x的函数
    （Ⅱ）根据直方图估计利润T不少于57000元的概率;
    （Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率（例如：若x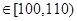,则取x=105，且x=105的概率等于需求量落入[100，110，求T的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为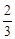，中奖可以获得2分；方案乙的中奖率为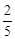，中奖可以获得3分；未中奖则不得分。每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品。
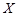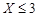    （Ⅰ）若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为,求的概率；
    （Ⅱ）若小明、小红两人都选择方案甲或都选择方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了响应学校“学科文化节”活动，数学组举办了一场数学知识比赛，共分为甲、乙两组．其中甲组得满分的有1个女生和3个男生，乙组得满分的有2个女生和4个男生．现从得满分的学生中，每组各任选2个学生，作为数学组的活动代言人．
    （1）求选出的4个学生中恰有1个女生的概率；（2）设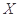为选出的4个学生中女生的人数，求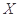的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某果园要用三辆汽车将一批水果从所在城市E运至销售城市F，已知从城市E到城市F有两条公路．统计表明：汽车走公路Ⅰ堵车的概率为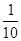，不堵车的概率为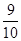；走公路Ⅱ堵车的概率为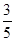，不堵车的概率为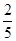，若甲、乙两辆汽车走公路Ⅰ，第三辆汽车丙由于其他原因走公路Ⅱ运送水果，且三辆汽车是否堵车相互之间没有影响．
    (1)求甲、乙两辆汽车中恰有一辆堵车的概率；
    (2)求三辆汽车中至少有两辆堵车的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

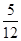    袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率为，得到黑球或黄球的概率是，得到黄球或绿球的概率是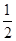，试求得到黑球、黄球、绿球的概率各是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两人参加某种选拔测试．在备选的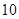道题中，甲答对其中每道题的概率都是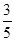，乙能答对其中的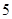道题．规定每次考试都从备选的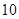道题中随机抽出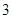道题进行测试，答对一题加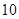分，答错一题（不答视为答错）减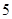分，至少得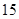分才能入选．
    （1）求甲得分的数学期望；
    （2）求甲、乙两人同时入选的概率．

    查看答案和解析>>

    同步练习册答案