
分析 (1)当|PM|最小时sinAPM最大,即∠APM最大,亦即∠APB最大,此时MP⊥l.
(2)在直线l:x+y+2=0上任取一点P(t,-t-2),以MP为直径的圆的方程为(x-1)(x-t)+(y-1)(y+t+2)=0,即x2+y2-(t+1)x+(t+1)y-2=0,求出过两圆x2+y2-(t+1)x+(t+1)y-2=0和x2+y2-2x-2y=0交点的直线AB的方程,即可得出结论.
解答 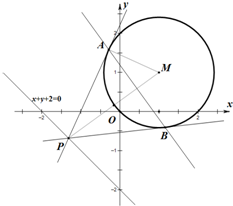 解:(1)如图,在直角三角形MPA中,$|AM|=\sqrt{2}$,∠APM是锐角,由$sinAPM=\frac{|AM|}{|PM|}=\frac{{\sqrt{2}}}{|PM|}$,当|PM|最小时sinAPM最大,即∠APM最大,亦即∠APB最大,此时MP⊥l.
解:(1)如图,在直角三角形MPA中,$|AM|=\sqrt{2}$,∠APM是锐角,由$sinAPM=\frac{|AM|}{|PM|}=\frac{{\sqrt{2}}}{|PM|}$,当|PM|最小时sinAPM最大,即∠APM最大,亦即∠APB最大,此时MP⊥l.
当MP⊥l时,直线MP的方程为 y=x,
由$\left\{\begin{array}{l}y=x\\ x+y+2=0\end{array}\right.$得 x=y=-1,所以点P的坐标为P(-1,-1),直线AB通过以PM为直径的圆与圆M的交点
以PM为直径的圆的方程为 (x-1)(x+1)+(y-1)(y+1)=0,即x2+y2=2,
过圆x2+y2=2与圆(x-1)2+(y-1)2=2交点的直线AB的方程为:x+y-1=0
点M到直线AB的距离为$\frac{1}{{\sqrt{2}}}$,$|AB|=\sqrt{6}$,点P到AB的距离为$\frac{3}{{\sqrt{2}}}$,所以,△PAB的面积为 ${S_{△PAB}}=\frac{1}{2}×\sqrt{6}×\frac{3}{{\sqrt{2}}}=\frac{{3\sqrt{3}}}{2}$.…(6分)
(2)在直线l:x+y+2=0上任取一点P(t,-t-2),以MP为直径的圆的方程为(x-1)(x-t)+(y-1)(y+t+2)=0,即x2+y2-(t+1)x+(t+1)y-2=0
过两圆x2+y2-(t+1)x+(t+1)y-2=0和x2+y2-2x-2y=0交点的直线AB的方程为(1-t)x+(t+3)y-2=0,即(y-x)t+x+3y-2=0,由$\left\{\begin{array}{l}y-x=0\\ x+3y-2=0\end{array}\right.$得$x=y=\frac{1}{2}$,所以,直线AB通过定点$(\frac{1}{2},\frac{1}{2})$.…(6分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
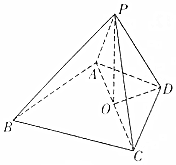 如图所示,四棱锥P-ABCD,△ABC为边长为2的正三角形,CD=$\sqrt{3}$,AD=1,PO垂直于平面ABCD于O,O为AC的中点,PO=1,求:
如图所示,四棱锥P-ABCD,△ABC为边长为2的正三角形,CD=$\sqrt{3}$,AD=1,PO垂直于平面ABCD于O,O为AC的中点,PO=1,求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com