
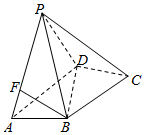
 四棱锥P-ABCD中,平面PAD⊥平面ABCD,△BCD的边长为$\sqrt{3}$的等边三角形,AD=2,AB=1,点F在线段AP上.
四棱锥P-ABCD中,平面PAD⊥平面ABCD,△BCD的边长为$\sqrt{3}$的等边三角形,AD=2,AB=1,点F在线段AP上.分析 (Ⅰ)根据面面垂直的性质定理证明平面PAD⊥平面ABCD即可证明CD⊥平面PAD;
(Ⅱ)根据点到平面的距离的定义作出点F到平面的距离,结合三角形的边角关系进行求解即可.
解答 解:(Ⅰ)∵AB=1,AD=2,BD=$\sqrt{3}$,
∴cos∠ADB=$\frac{A{D}^{2}+B{D}^{2}-A{B}^{2}}{2AD•BD}$=$\frac{\sqrt{3}}{2}$,
则∠ADB=30°,
∵△BCD是等边三角形,∴∠BDC=60°,
∴∠ADC=∠ADB+∠BDC=90°,即CD⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
CD?平面ABCD,
∴CD⊥平面PAD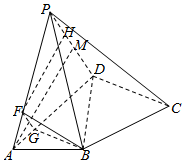
(Ⅱ) 在平面ABCD内过B作BG∥CD,交AD于G,BG?平面PCD,CD?平面PCD,
则BG∥平面PCD,
由(1)得CD⊥AD,∴BG⊥AD,
连接GF,
∵BF∥平面PCD,BF,BG?平面FBG,BF∩BG=B,
∴平面FBG∥平面PCD,
∵平面PAD分别交平面FBG,PCD于FG,PD,
∴FG∥PD,
∴$\frac{PF}{PA}=\frac{DG}{DA}$,
则直角三角形BGD中,BD=$\sqrt{3}$,∠BDG=30°,
DG=BDcos30°=$\frac{3}{2}$,
∴$\frac{PF}{PA}=\frac{DG}{DA}$=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$,
在平面PAD内过F作FH⊥PD于H,
∵CD⊥平面PAD,面FHC?面PAD,
∴CD⊥FH,
∵PD,CD?平面PCD,PD∩CD=D,
∴FH⊥平面PCD于H,
则FH是点F到平面PCD的距离.
过A作AM⊥PD于M,
∵△PAD是边长为2的等边三角形,
∴AM=$\frac{\sqrt{3}}{2}×2$=$\sqrt{3}$,
∵FH∥AM,∴$\frac{FH}{AM}$=$\frac{PF}{PA}=\frac{DG}{DA}$=$\frac{3}{4}$,
∴FH=$\frac{3}{4}$AM=$\frac{3\sqrt{3}}{4}$,
即点F到平面PCD的距离是$\frac{3\sqrt{3}}{4}$.
点评 本题主要考查考查空间直线和平面垂直的判断以及点到直线的距离的计算,根据相应的判定定理和性质定理以及点到平面的距离的定义是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
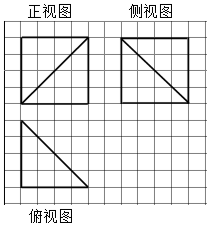 如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )| A. | $\frac{32}{3}$ | B. | 16 | C. | $\frac{64}{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
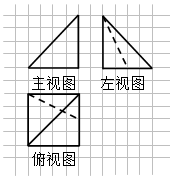 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,则该四棱锥的四个侧面中面积最大的一个侧面的面积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,则该四棱锥的四个侧面中面积最大的一个侧面的面积为( )| A. | 8$\sqrt{6}$ | B. | 8$\sqrt{2}$ | C. | 8 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个用斜二测法画出的水平放置的平面直观图,是一个直角梯形,O′A=5,AB=2,BD=3,∠O′AB=∠ABD=90°,则它的实际图形和面积分别是( )
如图,一个用斜二测法画出的水平放置的平面直观图,是一个直角梯形,O′A=5,AB=2,BD=3,∠O′AB=∠ABD=90°,则它的实际图形和面积分别是( )| A. | 直角梯形、面积是16$\sqrt{2}$ | B. | 直角梯形、面积是8 | ||
| C. | 梯形非直角,面积是16 | D. | 梯形非直角,面积是8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com