
【题目】据市场调查发现,某种产品在投放市场的30天中,其销售价格![]() (元)和时间
(元)和时间![]() (天)的关系如图所示.
(天)的关系如图所示.

(1)求销售价格![]() (元)和时间
(元)和时间![]() (天)的函数关系式;
(天)的函数关系式;
(2)若日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系式是
(天)的函数关系式是![]()
![]() ,问该产品投放市场第几天时,日销售额
,问该产品投放市场第几天时,日销售额![]() (元)最高,且最高为多少元?
(元)最高,且最高为多少元?
【答案】(Ⅰ)![]() ;(Ⅱ)在第10天时,日销售额最大,最大值为900元.
;(Ⅱ)在第10天时,日销售额最大,最大值为900元.
【解析】
试题(Ⅰ)通过讨论t的范围,求出函数的表达式即可;(Ⅱ)先求出函数的表达式,通过讨论t的范围,求出函数的最大值即可.
解:(Ⅰ)①当0≤t<20,t∈N时,
设P=at+b,将(0,20),(20,40)代入,得![]() 解得
解得![]()
所以P=t+20(0≤t<20,t∈N).
②当20≤t≤30,t∈N时,
设P=at+b,将(20,40),(30,30)代入,解得![]()
所以 P=﹣t+60(20≤t≤30,t∈N),)
综上所述![]()
(Ⅱ)依题意,有y=PQ,
得![]()
化简得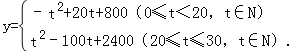
整理得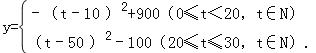
①当0≤t<20,t∈N时,由y=﹣(t﹣10)2+900可得,当t=10时,y有最大值900元.
②当20≤t≤30,t∈N时,由y=(t﹣50)2﹣100可得,当t=20时,y有最大值800元.
因为 900>800,所以在第10天时,日销售额最大,最大值为900元.


科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,已知a≠b,cos2A﹣cos2B= ![]() sinAcosA﹣
sinAcosA﹣ ![]() sinBcosB. (Ⅰ)求角C的大小;
sinBcosB. (Ⅰ)求角C的大小;
(Ⅱ)若c= ![]() ,siniA=
,siniA= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇为了提高当地地方经济总量,决定引进资金对原有的两个企业![]() 和
和![]() 进行改造,计划每年对两个企业共投资500万元,要求对每个企业至少投资50万元.根据已有经验,改造后
进行改造,计划每年对两个企业共投资500万元,要求对每个企业至少投资50万元.根据已有经验,改造后![]() 企业的年收益
企业的年收益![]() (单位:万元)和
(单位:万元)和![]() 企业的年收益
企业的年收益![]() (单位:万元)与投入资金
(单位:万元)与投入资金![]() (单位:万元)分别满足关系式:
(单位:万元)分别满足关系式:![]() ,
,![]() .设对
.设对![]() 企业投资额为
企业投资额为![]() (单位:万元),每年两个企业的总收益为
(单位:万元),每年两个企业的总收益为![]() (单位:万元).
(单位:万元).
(1)求![]() ;
;
(2)试问如何安排两个企业的投入资金,才能使两个企业的年总收益达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=2an+1(n∈N*).
(1)求数列{an}的通项公式;
(2)设Sn为数列{ ![]() }的前n项和,求证:1≤Sn<4.
}的前n项和,求证:1≤Sn<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k为常数,e为自然对数的底数),曲线
(k为常数,e为自然对数的底数),曲线![]() 在点(1, f (1))处的切线与x轴平行.
在点(1, f (1))处的切线与x轴平行.
(1)求k的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() 其中
其中![]() 为
为![]() 的导函数,证明:对任意
的导函数,证明:对任意![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊亚历山大时期的数学家帕普斯(Pappus,约300~约350)在《数学汇编》第3卷中记载着一个定理:“如果同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以重心旋转所得周长的积.”如图,半圆![]() 的直径
的直径![]() ,点
,点![]() 是该半圆弧的中点,半圆弧与直径
是该半圆弧的中点,半圆弧与直径![]() 所围成的半圆面(阴影部分不含边界)的重心
所围成的半圆面(阴影部分不含边界)的重心![]() 位于对称轴
位于对称轴![]() 上.若半圆面绕直径
上.若半圆面绕直径![]() 所在直线旋转一周,则所得到的旋转体的体积为__________
所在直线旋转一周,则所得到的旋转体的体积为__________![]() ,
,![]() ___________________
___________________![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com