
分析 由题意知由细到粗每段的重量成等差数列,记为{an}且设公差为d,由条件和等差数列的通项公式列出方程组,求出a1和d值,由等差数列的前n项和公式求出该金杖的总重量M,代入已知的式子化简求出i的值.
解答 解:由题意知由细到粗每段的重量成等差数列,
记为{an},设公差为d,
则$\left\{\begin{array}{l}{{a}_{1}+{a}_{2}=2}\\{{a}_{9}+{a}_{10}=4}\end{array}\right.$,解得a1=$\frac{15}{16}$,d=$\frac{1}{8}$,
所以该金杖的总重量M=$10×\frac{15}{16}+\frac{10×9}{2}×\frac{1}{8}$=15,
因为48ai=5M,所以48[$\frac{15}{16}$+(i-1)×$\frac{1}{8}$]=25,
即39+6i=75,解得i=6,
故答案为:6.
点评 本题考查等差数列的通项公式、前n项和公式的实际应用,以及方程思想,考查化简、计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{5}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,$\frac{5}{2}$] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | (0,$\frac{1}{2}$] | D. | [$\frac{2}{5}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x | B. | y2=8x | C. | y2=3x | D. | y2=6x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
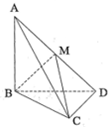 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com