
分析 (1)把m=4代入B中方程求出解,确定出B,求出A中方程的解确定出A,找出两集合的并集即可;
(2)由B为A的子集,分B为空集与B不为空集两种情况求出m的范围即可.
解答 解:(1)由A中方程解得:x=4,即A={4};
将m=4代入B中的方程得:x2-10x+16=0,即(x-2)(x-8)=0,
解得:x=2或x=8,即B={2,8},
则A∪B={2,4,8};
(2)∵A∪B=A,∴B⊆A或B=A,
∴当B=∅时,则有△=4(m+1)2-4m2<0,即m<-$\frac{1}{2}$;
当B=A时,则△=4(m+1)2-4m2=0,且-$\frac{-2(m+1)}{2}$=4
解得:m不存在;
故m<-$\frac{1}{2}$.
点评 此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [9,49] | B. | (17,49] | C. | [9,41] | D. | (17,41] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
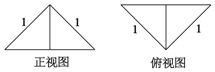 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com