
分析 (1)根据数列递推公式即可证明,
(2)先求出数列{bn}的通项公式,再分类求出{an}的通项公式,
(3)令S=1•21+2•22+…+n•2n根据错位相减法求出Sn,分离参数,根据数列的函数特征即可求出λ的取值范围.
解答 解:(1)${b_{n+1}}={a_{2n+2}}-1=2{a_{2n+1}}-3(-1{)^{2n+1}}-1=2{a_{2n+1}}+2$=$4{a_{2n}}-6(-1{)^{2n}}+2=4{a_{2n}}-4=4{b_n}$…(3分)
(2)a2=2a1-3(-1)=5,b1=a2-1=4,因为bn+1=4bn
所以$\frac{{{b_{n+1}}}}{b_n}=4$,所以{bn}是等比数列,所以bn=4n=a2n-1,${a_{2n}}={4^n}+1={2^{2n}}+1$,${a_{2n}}=2{a_{2n-1}}+3={2^{2n}}+1$,${a_{2n-1}}={2^{2n-1}}-1$
所以${a_n}=\left\{\begin{array}{l}{2^n}-1,n为奇数\\{2^n}+1,n为偶数\end{array}\right.$,即${a_n}={2^n}+(-1{)^n}$…(8分)
(3)由(2)$n{a_n}=n•{2^n}+(-1{)^n}•n$,
$\begin{array}{l}{S_n}={a_1}+2{a_2}+3{a_3}+…+n{a_n}=(1•{2^1}-1)+(2•{2^n}+2)+…+(n•{2^n}+{(-1)^n}•n)\\=(1•{2^1}+2•{2^n}+…+n•{2^n})+(-1+2-3+…+{(-1)^n}•n)\end{array}$
令S=1•21+2•22+…+n•2n
则2S=1•22+2•23+…+(n-1)•2n+n•2n+1$-S={2^1}+{2^2}+…+{2^n}-n•{2^{n+1}}=\frac{{2-{2^{n+1}}}}{1-2}-n•{2^{n+1}}$,
S=(n-1)•2n+1+2…(9分)
n为奇数时,$T=-1+2-3+…+{(-1)^n}•n=-\frac{n+1}{2}$,
n为偶数时,$T=-1+2-3+…+{(-1)^n}•n=\frac{n}{2}$…(11分)
所以n为奇数时${S_n}=S+T=(n-1)•{2^{n+1}}+2-\frac{n+1}{2}>λ{2^n}$,
即$λ<2(n-1)+\frac{3-n}{{2•{2^n}}}$恒成立,
易证$2(n-1)+\frac{3-n}{{2•{2^n}}}$递增,n=1时$2(n-1)+\frac{3-n}{{2•{2^n}}}$取最小值$\frac{1}{2}$,
所以$λ<\frac{1}{2}$n为偶数时,
${S_n}=S+T=(n-1)•{2^{n+1}}+2+\frac{n}{2}>λ{2^n}$,
即$λ<2(n-1)+\frac{4+n}{{2•{2^n}}}$,
易证$2(n-1)+\frac{4+n}{{2•{2^n}}}$递增,n=2时$2(n-1)+\frac{4+n}{{2•{2^n}}}$取最小值$\frac{11}{4}$,
所以$λ<\frac{11}{4}$…(15分)
综上可得 $λ<\frac{1}{2}$.(16分)
点评 本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,对数学思维的要求比较高,要注意错位相减求和法和转化与化归思想的合理运用,本题有一定的探索性.综合性强,难度大,易出错.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
 为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.| 不常喝 | 常喝 | 合计 | |
| 肥胖 | x | y | 50 |
| 不肥胖 | 40 | 10 | 50 |
| 合计 | A | B | 100 |
| P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{5}^{2}$×A${\;}_{4}^{3}$种 | B. | A${\;}_{5}^{2}$×43种 | C. | C${\;}_{5}^{2}$×A${\;}_{4}^{3}$种 | D. | C${\;}_{5}^{2}$×43种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
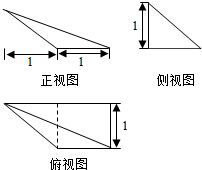 某几何体的三视图如图所示,则该几何体的各侧面中,面积最小值为( )
某几何体的三视图如图所示,则该几何体的各侧面中,面积最小值为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com