
分析 首先由函数单调性定义,判断f(x)=x|x-a|在[-2,+∞)上单调递增;
然后把a分成a≤-2与a>-2两种情况分别进行检验;
应当注意的是当a>-2时,应当分类讨论,讨论a是否为0,否则会使答案漏解.
解答 解:由题意知,对于任意的x1,x2∈[-2,+∞),x1≠x2,
不等式$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$>0恒成立,
∴f(x)=x|x-a|在[-2,+∞)上单调递增.
(1)当a≤-2时,
若x∈[-2,+∞),则f(x)=x(x-a)=x2-ax,其对称轴为x=$\frac{a}{2}$,
此时$\frac{a}{2}$≤-2,所以f(x)在[-2,+∞)上是递增的;
即a≤-4时满足题意;
(2)当a>-2且a≠0时,
①若x∈[a,+∞),则f(x)=x(x-a)=x2-ax,其对称轴为x=$\frac{a}{2}$,所以f(x)在[a,+∞)上是递增的;
②若x∈[-2,a),则f(x)=x(a-x)=-x2+ax,其对称轴为x=$\frac{a}{2}$,所以f(x)在[$\frac{a}{2}$,a)上是递减的,
因此f(x)在[-2,a)上必有递减区间.
故可知当a>-2且a≠0时不成立,故舍去;
(3)当a=0时,可知函数为f(x)=x|x|=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,
由二次函数的性质可知,符合题意单调递增的要求,故成立
综上,实数a的取值范围是(-∞,-4]∪{0}.
点评 本题考查了函数单调性的定义,考查了分类讨论的思想方法,正确的进行分类讨论是解好本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
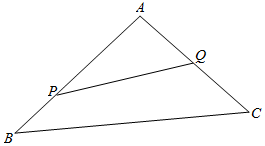 如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com