
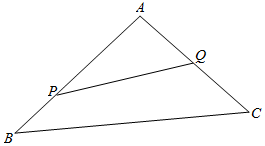
 如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏.分析 (1)依题意,∠AQP=45°,由正弦定理:$\frac{AP}{{sin{{45}°}}}=\frac{AQ}{{sin{{15}°}}}=\frac{PQ}{{sin{{120}°}}}$,可得$\frac{AP+AQ}{{sin{{45}°}+sin{{15}°}}}=\frac{PQ}{{sin{{120}°}}}$利用特殊角的三角函数值即可计算得解PQ的值.
(2)设AP=x米,AQ=y米,利用三角形面积公式可求xy=10000,进而可求$x+y≥2\sqrt{xy}=200$,设△ABC的周长为L,则L=$x+y+\sqrt{{x^2}+{y^2}+xy}$=$x+y+\sqrt{{{(x+y)}^2}-10000}$,令x+y=t,L=$t+\sqrt{{t^2}-10000}$在定义域上单调增,利用二次函数的图象和性质即可得解.
解答 (本题满分为16分)
解:(1)∵依题意,∠AQP=45°,由正弦定理:$\frac{AP}{{sin{{45}°}}}=\frac{AQ}{{sin{{15}°}}}=\frac{PQ}{{sin{{120}°}}}$,…(2分)
∴得$\frac{AP+AQ}{{sin{{45}°}+sin{{15}°}}}=\frac{PQ}{{sin{{120}°}}}$,…(3分)
∵$sin{15°}=sin({45°}-{30°})=sin{45°}cos{30°}-cos{45°}sin{30°}=\frac{{\sqrt{6}-\sqrt{2}}}{4}$,…(5分)
∴$\frac{AP+AQ}{{sin{{45}°}+sin{{15}°}}}=\frac{PQ}{{sin{{120}°}}}=\frac{{100(\sqrt{3}+1)}}{{\frac{{\sqrt{6}+\sqrt{2}}}{4}}}$$⇒PQ=100\sqrt{6}$…(7分)
(2)设AP=x米,AQ=y米.
则$S=\frac{1}{2}xysin{120°}=2500\sqrt{3}$⇒xy=10000,…(9分)
$x+y≥2\sqrt{xy}=200$,…(11分)
设△ABC的周长为L,则L=$x+y+\sqrt{{x^2}+{y^2}+xy}$=$x+y+\sqrt{{{(x+y)}^2}-10000}$,…(12分)
令x+y=t,L=$t+\sqrt{{t^2}-10000}$在定义域上单调增,
所以${L_{min}}=200+100\sqrt{3}$,当x=y=100取等号;…(15分)
答:(1)$PQ=100\sqrt{6}$米;
(2)当AP=AQ=100米时,三角形地块APQ的周长最小.…(16分)
点评 本题考查利用数学知识解决实际问题,考查三角形面积的计算,余弦定理,二次函数的图象和性质的运用,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{C}_{3}^{2}}{{C}_{50}^{2}}$ | B. | $\frac{{C}_{3}^{1}{C}_{47}^{1}}{{C}_{50}^{2}}$ | C. | $\frac{{C}_{47}^{2}}{{C}_{50}^{2}}$ | D. | 1-$\frac{{C}_{47}^{2}}{{C}_{50}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
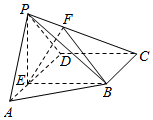 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com