
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用向量的基本知识进行分析转化是解决本题的关键.根据向量的数乘运算、向量的数量积运算性质,向量减法的几何意义对有关问题进行求解并加以判断.
解答 解:对于①($\overrightarrow{a}$•$\overrightarrow{b}$)2=$\overrightarrow{a}$2$\overrightarrow{b}$2cos2<$\overrightarrow{a}$,$\overrightarrow{b}$>,故①不正确,
对于②,根据向量的几何意义可得,|$\overrightarrow{a}$+$\overrightarrow{b}$|≥|$\overrightarrow{a}$-$\overrightarrow{b}$|不正确,
对于③,|$\overrightarrow{a}$+$\overrightarrow{b}$|2=($\overrightarrow{a}$+$\overrightarrow{b}$)2,正确
对于④[($\overrightarrow{b}$•$\overrightarrow{c}$)$\overrightarrow{a}$-($\overrightarrow{c}$•$\overrightarrow{a}$)$\overrightarrow{b}$]•$\overrightarrow{c}$=($\overrightarrow{b}$•$\overrightarrow{c}$)($\overrightarrow{a}$$•\overrightarrow{c}$)-($\overrightarrow{c}$•$\overrightarrow{a}$)($\overrightarrow{b}$•$\overrightarrow{c}$)=0故④中两向量垂直,故④不正确,
故选:A.
点评 本题考查平面向量的基本运算性质,数量积的运算性质,考查向量问题的基本解法,等价转化思想.要区分向量运算与数的运算.避免类比数的运算进行错误选择.


科目:高中数学 来源: 题型:填空题
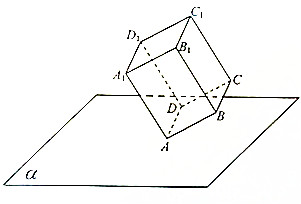 如图,直四棱柱ABCD-A1B1C1D1底面是边长为1的正方形,高AA1=$\sqrt{2}$,点A是平面α内的一个定点,AA1与α所成角为$\frac{π}{3}$,点C1在平面α内的射影为P,当四棱柱ABCD-A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积=$2\sqrt{3}π$.
如图,直四棱柱ABCD-A1B1C1D1底面是边长为1的正方形,高AA1=$\sqrt{2}$,点A是平面α内的一个定点,AA1与α所成角为$\frac{π}{3}$,点C1在平面α内的射影为P,当四棱柱ABCD-A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积=$2\sqrt{3}π$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为1的奇函数 | B. | 周期为2的偶函数 | ||
| C. | 周期为1的非奇非偶函数 | D. | 周期为2的非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com