
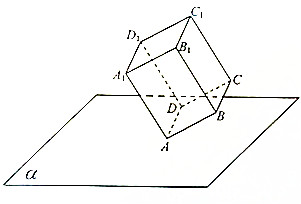
 如图,直四棱柱ABCD-A1B1C1D1底面是边长为1的正方形,高AA1=$\sqrt{2}$,点A是平面α内的一个定点,AA1与α所成角为$\frac{π}{3}$,点C1在平面α内的射影为P,当四棱柱ABCD-A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积=$2\sqrt{3}π$.
如图,直四棱柱ABCD-A1B1C1D1底面是边长为1的正方形,高AA1=$\sqrt{2}$,点A是平面α内的一个定点,AA1与α所成角为$\frac{π}{3}$,点C1在平面α内的射影为P,当四棱柱ABCD-A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积=$2\sqrt{3}π$. 分析 由题意,点A是平面α内的一个定点,AA1与α所成角为$\frac{π}{3}$,四棱柱ABCD-A1B1C1D1按要求运动,为A定点的旋转运动和定直线AA1旋转运动.再作点C1在平面α内的射影为P的轨迹扫过的图形,即可得到点P所经过的区域的面积.
解答 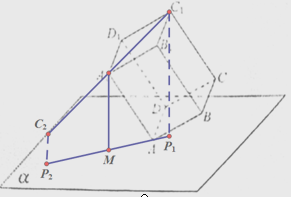
解:当长方体绕A1A转的时候,C1C形成一个圆柱,过C1往平面α作垂线垂足P,就形成一个椭圆,其短轴为P1P2=$\sqrt{6}$,长轴为$2\sqrt{2}$ 的y型的椭圆,其中心A点在平面α上的射影M.
当AA1绕着A点转时,则椭圆就以A为圆心,$\frac{\sqrt{2}}{2}$为半径的圆上运动,其扫过的区域为一个圆环,外径为$\frac{\sqrt{2}+\sqrt{6}}{6}$,内径为$\frac{\sqrt{6}-\sqrt{2}}{2}$,
所以面积为:[($\frac{\sqrt{2}+\sqrt{6}}{6}$)2-$(\frac{\sqrt{6}-\sqrt{2}}{2})^{2}$]•π=$2\sqrt{3}π$
故填:$2\sqrt{3}π$.
点评 本题考查了立体几何中以定点旋转和定直线旋转运动形成的图形的面积问题.注重空间思维的想象力的培养和作图能力,数形结合和转化的思想的灵活性的运用.属于难题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{7\sqrt{2}}}{10}$ | B. | $\frac{{7\sqrt{2}}}{10}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com