
分析 (Ⅰ)n=1时,a1=1,当n≥2时,${S_{n-1}}=\frac{{{a_{n-1}}({a_{n-1}}+1)}}{2}(n≥2)$,与原式相减,即可求得(an+an-1)(an-an-1)=(an+an-1),由an+an-1≠0,an-an-1=1(n≥2),∴数列{an}是首项为1公差为1的等差数列;
(Ⅱ)由(Ⅰ)可知,${S_n}=\frac{{{n^2}+n}}{2}$,${b_n}=\frac{2}{{{n^2}+n}}=\frac{2}{n(n+1)}=2({\frac{1}{n}-\frac{1}{n+1}})$,采用“裂项法”即可求得${T_n}=\frac{2}{{1+\frac{1}{n}}}$,由函数单调性可知,Tn≥T1=1,可求得λ≤1.
解答 解:(Ⅰ)n=1时,a1=1,
${S_n}=\frac{{{a_n}({a_n}+1)}}{2}(n∈{N^*})$①
当n≥2时,${S_{n-1}}=\frac{{{a_{n-1}}({a_{n-1}}+1)}}{2}(n≥2)$②
①-②得:${a_n}=\frac{{{a_n}^2+{a_n}-{a_{n-1}}^2-{a_{n-1}}}}{2}$(n≥2),
整理得:(an+an-1)(an-an-1)=(an+an-1),
∵数列{an}的各项均为正数,
∴an+an-1≠0,
∴an-an-1=1(n≥2),
∴数列{an}是首项为1公差为1的等差数列; (6分)
(Ⅱ)由(1)得:${S_n}=\frac{{{n^2}+n}}{2}$,
∴${b_n}=\frac{2}{{{n^2}+n}}=\frac{2}{n(n+1)}=2({\frac{1}{n}-\frac{1}{n+1}})$,
∴${T_n}=2[{(1-\frac{1}{2})+({\frac{1}{2}-\frac{1}{3}})+({\frac{1}{3}-\frac{1}{4}})+…+(\frac{1}{n}-\frac{1}{n+1})}]=2({1-\frac{1}{n+1}})=\frac{2n}{n+1}$,
∵${T_n}=\frac{2}{{1+\frac{1}{n}}}$,
∴Tn单调递增,
∴Tn≥T1=1,
∴λ≤1.(12分)
点评 本题考查等差数列通项公式的求法,考查采用“裂项法”求数列的前n项和,考查利用函数单调性求实数λ的取值范围,考查计算能力,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
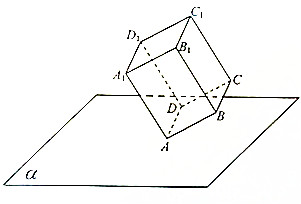 如图,直四棱柱ABCD-A1B1C1D1底面是边长为1的正方形,高AA1=$\sqrt{2}$,点A是平面α内的一个定点,AA1与α所成角为$\frac{π}{3}$,点C1在平面α内的射影为P,当四棱柱ABCD-A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积=$2\sqrt{3}π$.
如图,直四棱柱ABCD-A1B1C1D1底面是边长为1的正方形,高AA1=$\sqrt{2}$,点A是平面α内的一个定点,AA1与α所成角为$\frac{π}{3}$,点C1在平面α内的射影为P,当四棱柱ABCD-A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积=$2\sqrt{3}π$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com