
已知函数f(x)=ln x-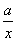 .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)<x2在(1,+∞)上恒成立,求a的取值范围.
解:(1)由题意知f(x)的定义域为(0,+∞),
且f′(x)=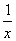 +
+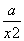 =
= .
.
∵a>0,∴f′(x)>0,
故f(x)在(0,+∞)上是单调递增函数.
(2)∵f(x)<x2,∴ln x-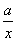 <x2.
<x2.
又x>0,∴a>xln x-x3.
令g(x)=xln x-x3,
h(x)=g′(x)=1+ln x-3x2,
h′(x)=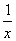 -6x=
-6x=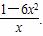 .
.
∵x∈(1,+∞)时,h′(x)<0,
∴h(x)在(1,+∞)上是减函数.
∴h(x)<h(1)=-2<0,即g′(x)<0,
∴g(x)在(1,+∞)上也是减函数.
g(x)<g(1)=-1,∴当a≥-1时,f(x)<x2在(1,+∞)上恒成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图像在x=1处的切线平行于直线6x+2y+5=0,则f(x)极大值与极小值之差为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)=x3-3x-1,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
A.20 B.18
C.3 D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
在高校自主招生中,某校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名,并且北京大学和清华大学都要求必须有男生参加,学校通过选拔定下3男2女共5个推荐对象,则不同推荐方法的种数是 ( )
A.20 B.22 C.24 D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com