
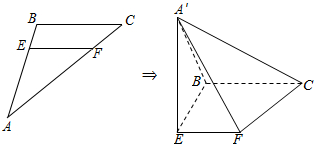
 已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AE=2EB,AF=2FC,将△AEF沿EF折起,使A变到A′,使平面A′EF⊥平面EFCB.
已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AE=2EB,AF=2FC,将△AEF沿EF折起,使A变到A′,使平面A′EF⊥平面EFCB.分析 (1)由AE=2EB,AF=2FC,可得EF∥BC,且EF=$\frac{2}{3}BC$,在底面BEFC中,过F作FG∥EB,交BC于G,在平面A′BC中,过G作GH∥A′B交A′C于H,连接FH,由面面平行的判定可得平面HGF∥面A′BE,从而得到FH∥平面A′BE,且$A′H=\frac{2}{3}A′C$;
(2)由题意可得三棱锥A′-EBC的三个侧面和底面均为直角三角形,求解个直角三角形面积,作和后可得三棱锥A′-EBC的表面积;
在直角三角形EBC中,取EC中点K,则KE=KB=KC,过K作KO∥A′E交A′C于O,则O为A′C的中点,此时OA′=OE=OB=OC,即OA′为三棱锥A′-EBC的外接球的半径,求解直角三角形得三棱锥A′-EBC的外接球的半径.
解答 解:(1)如图
在Rt△ABC中,AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AE=2EB,AF=2FC,
∴EF∥BC,且EF=$\frac{2}{3}BC$,
在底面BEFC中,过F作FG∥EB,交BC于G,
在平面A′BC中,过G作GH∥A′B交A′C于H,连接FH,
∵FG∥EB,BE?面A′BE,FG?面A′BE,
∴FG∥面A′BE.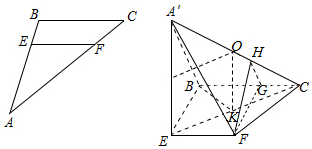
∵GH∥A′B,A′B?面A′BE,HG?面A′BE,
∴HG∥面A′BE,
又HG∩FG=G,
∴平面HGF∥面A′BE,
则FH∥平面A′BE,
由EF=BG=$\frac{2}{3}BC$,可得$A′H=\frac{2}{3}A′C$;
(2)A′E=2,BE=1,BC=4,
∵∠EBC=90°,
∴$EC=\sqrt{B{E}^{2}+B{C}^{2}}=\sqrt{17}$,$A′B=\sqrt{5}$,
由A′EF⊥平面EFCB,且A′E⊥EF,
可得A′E⊥平面EFCB,
∴△A′EB,△A′EC为Rt△,
由面A′EB⊥平面EFCB,
BC⊥BE,可得A′B⊥BC,
则△A′BC,△EBC为Rt△,
∴三棱锥A′-EBC的表面积为$\frac{1}{2}(1×4+1×2+4×\sqrt{5}+2×\sqrt{17})$=$3+2\sqrt{5}+\sqrt{17}$;
在直角三角形EBC中,取EC中点K,
则KE=KB=KC,过K作KO∥A′E交A′C于O,
则O为A′C的中点,此时OA′=OE=OB=OC,
即OA′为三棱锥A′-EBC的外接球的半径,等于$\frac{1}{2}A′C=\frac{1}{2}\sqrt{{2}^{2}+17}=\frac{1}{2}\sqrt{21}$.
点评 本题考查平面图形的折叠问题,考查了直线与平面平行的判定,考查棱锥体积的求法,考查了空间想象能力和思维能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 11 | C. | 15 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com