
| A. | {a1|a1≥2017,a1∈N+} | B. | {a1|a1≥2016,a1∈N+} | C. | {a1|a1≥2015,a1∈N+} | D. | {a1|a1≥2014,a1∈N+} |
分析 数列{an}满足${a_{n+1}}=\sqrt{{a_n}^2-2{a_n}+2}+1(n∈{N_+})$,可得$({a}_{n+1}-1)^{2}$-$({a}_{n}-1)^{2}$=1,an+1≥2.不等式a2016>2017化为:$\sqrt{({a}_{1}-1)^{2}+2015}$+1≥2017,进而得出.
解答 解:∵数列{an}满足${a_{n+1}}=\sqrt{{a_n}^2-2{a_n}+2}+1(n∈{N_+})$,
∴$({a}_{n+1}-1)^{2}$-$({a}_{n}-1)^{2}$=1,an+1≥2.
∴$({a}_{n}-1)^{2}$=$({a}_{1}-1)^{2}$+(n-1).
则不等式a2016>2017化为:$\sqrt{({a}_{1}-1)^{2}+2015}$+1≥2017,
∴$({a}_{1}-1)^{2}$≥20162-2015,解得a1≥2017.
∴则使不等式a2016>2017成立的所有正整数a1的集合为{a1|a1≥2017,a1∈N+}.
故选:A.
点评 本题考查了数列递推关系、等差数列的通项公式、不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
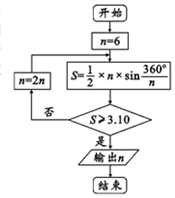 公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )
公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )| A. | 12 | B. | 24 | C. | 48 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $-\frac{8}{9}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},\sqrt{e}})$ | B. | $[{\frac{1}{2},\sqrt{e}})$ | C. | $({\frac{1}{2},\frac{{\sqrt{e}}}{e}}]$ | D. | $({\frac{1}{2},\frac{{\sqrt{e}}}{e}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com