
如图所示,在边长为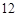 的正方形
的正方形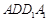 中,点
中,点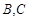 在线段
在线段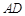 上,且
上,且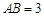 ,
,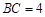 ,作
,作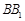 //
//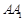 ,分别交
,分别交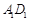 ,
,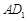 于点
于点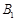 ,
,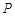 ,作
,作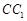 //
//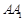 ,分别交
,分别交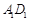 ,
,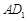 于点
于点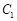 ,
,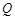 ,将该正方形沿
,将该正方形沿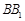 ,
,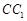 折叠,使得
折叠,使得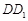 与
与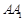 重合,构成如图所示的三棱柱
重合,构成如图所示的三棱柱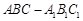 .
.
(1)求证: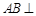 平面
平面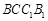 ;
;
(2)若点E为四边形BCQP内一动点,且二面角E-AP-Q的余弦值为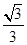 ,求|BE|的最小值.
,求|BE|的最小值.
(1)参考解析;(2)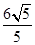
解析试题分析:(1)依题意可得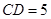 .即翻折后的
.即翻折后的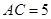 .所以由
.所以由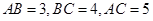 .可得
.可得 .又因为
.又因为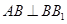 ,所以可得:
,所以可得: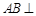 平面
平面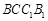 .
.
(2)依题意建立空间直角坐标系,由平面APQ写出其法向量.假设点E(m,n,0),根据平面APE写出其法向量.再由二面角E-AP-Q的余弦值为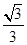 ,可得到关于m,n的方程m+2n-6=0.再由点B到直线的距离公式即可得到结论.
,可得到关于m,n的方程m+2n-6=0.再由点B到直线的距离公式即可得到结论.
(1)在正方形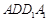 中,因为
中,因为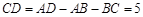 ,
,
所以三棱柱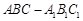 的底面三角形
的底面三角形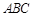 的边
的边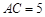 .
.
因为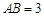 ,
,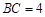 ,所以
,所以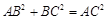 ,所以
,所以 .
.
因为四边形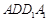 为正方形,
为正方形,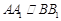 ,所以
,所以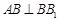 ,而
,而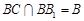 ,
,
所以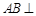 平面
平面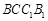 .----------- 4分
.----------- 4分
(2)因为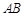 ,
, ,
,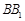 两两互相垂直.以
两两互相垂直.以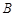 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系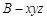 ,
,
则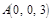 ,
, ,
,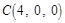 ,
, ,
,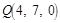 ,
,
所以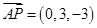 ,
,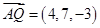 ,
,
设平面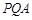 的一个法向量为
的一个法向量为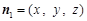 .
.
则由 ,即
,即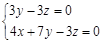 令
令 ,
,
则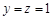 .所以
.所以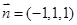 .
.
设点E(m,n,0),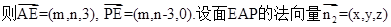

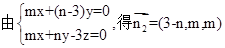 .由
.由 得:m+2n-6=0
得:m+2n-6=0
所以|BE|的最小值为点B到线段: m+2n-6="0" 的距离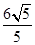 ------- 13分
------- 13分
考点:1.直线与平面的位置关系.2.二面角.3.空间直角坐标系的建立.4.点到直线的距离.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,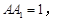
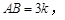
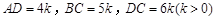 .
.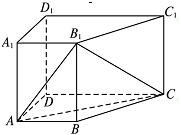
(Ⅰ)求证:CD⊥平面ADD1A1;
(Ⅱ)若直线AA1与平面AB1C所成角的正弦值为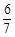 ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)(2011•重庆)如图,在四面体ABCD中,平面ABC⊥平面ACD,AB⊥BC,AC=AD=2,BC=CD=1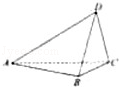
(Ⅰ)求四面体ABCD的体积;
(Ⅱ)求二面角C﹣AB﹣D的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知四棱锥P-ABCD的底面ABCD是菱形,且PC⊥平面ABCD,PC=AC=2,E是PA的中点。
(1)求证:AC⊥平面BDE;
(2)若直线PA与平面PBC所成角为30°,求二面角P-AD-C的正切值;
(3)求证:直线PA与平面PBD所成的角φ为定值,并求sinφ值。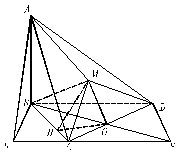
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com