
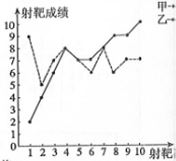
 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示| 平均数 | 方差 | 中位数 | 命中9环及以上 | |
| 甲 | 1.2 | 7 | ||
| 乙 | 3 |
分析 (I)运用折线对应的数据判断,填写表格.
(II)求解平均数,方差,中位数,众数,根据数字特征的意义判断分析.
解答 解:(I)填充后的表格如下:
| 平均数 | 方差 | 中位数 | 命中9环及以上 | |
| 甲 | 7 | 1.2 | 7 | 1 |
| 乙 | 7 | 5.4 | 7.5 | 3 |
点评 本题考察了综合运用数据,结合折线,表格等分析数据得出数字特征,解决分析问题,判断需要的答案.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a、b、c、d中至多有三个是正数 | B. | a、b、c、d中至多有两个是正数 | ||
| C. | a、b、c、d都是正数 | D. | a、b、c、d都是负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com