
分析 需要分类讨论:a+1<0、a+1=0、a+1>0三种情况下的集合M是否符合题意,由此求得a的取值范围.
解答 解:由已知得N={x|-3≤x≤1},M={x|x(x-a-1)<0(a∈R)},由已知M⊆N,得
①当a+1<0即a<-1时,集合M={x|a+1<x<0}.
要使M⊆N成立,只需-3≤a+1<0,解得-4≤a<-1;
②当a+1=0即a=-1时,M=∅,显然有M⊆N,所以a=-1符合题意.
③当a+1>0即a>-1时,集合M={x|0<x<a+1}.
要使M⊆N成立,只需0<a+1≤1,解得-1<a≤0,
综上所述,所以a的取值范围是[-4,0].
点评 本题考查集合的包含关系判断及应用,综合性强,具有一定的难度.解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
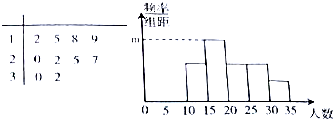 从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))
从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))查看答案和解析>>
科目:高中数学 来源: 题型:解答题
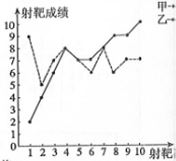 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示| 平均数 | 方差 | 中位数 | 命中9环及以上 | |
| 甲 | 1.2 | 7 | ||
| 乙 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知F1,F2分别为椭圆C1:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1的上、下焦点,F1是抛物线C1:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$
已知F1,F2分别为椭圆C1:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1的上、下焦点,F1是抛物线C1:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | algx>blgx(x>0) | B. | ax2>bx2 | C. | a2>b2 | D. | $\frac{a}{{{2^x}+1}}>\frac{b}{{{2^x}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com