
 已知F1,F2分别为椭圆C1:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1的上、下焦点,F1是抛物线C1:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$
已知F1,F2分别为椭圆C1:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1的上、下焦点,F1是抛物线C1:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$分析 (1)利用抛物线的方程和定义即可求出点M的坐标,再利用椭圆的定义即可求出;
(2)根据直线与圆相切则圆心到直线距离等于半径,可得k=$\frac{2t}{1-{t}^{2}}$,联立直线与椭圆方程,结合椭圆上一点P满足$\overrightarrow{OA}$+$\overrightarrow{OB}$=λ$\overrightarrow{OP}$,可得到λ2的表达式,进而求出实数λ的取值范围.
解答 解:(Ⅰ)由题知F1(0,1),所以a2-b2=1,
又由抛物线定义可知MF1=yM+1=$\frac{5}{3}$,得yM=$\frac{2}{3}$,
于是易知M(-$\frac{2\sqrt{6}}{3}$,$\frac{2}{3}$),从而MF1=$\sqrt{(\frac{2\sqrt{6}}{3})^{2}+(\frac{2}{3}+1)^{2}}$=$\frac{7}{3}$,
由椭圆定义知2a=MF1+MF2=4,得a=2,故b2=3,
从而椭圆的方程为$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1;
(Ⅱ)设A(x1,y1),B(x2,y2),P(x0,y0),则由$\overrightarrow{OA}$+$\overrightarrow{OB}$=λ$\overrightarrow{OP}$知,
x1+x2=λx0,y1+y2=λy0,且$\frac{{{x}_{0}}^{2}}{3}$+$\frac{{{y}_{0}}^{2}}{4}$=1,①
又直线l:y=k(x+t),kt≠0与圆x2+(y+1)2=1相切,所以有$\frac{|kt+1|}{\sqrt{1+{k}^{2}}}$=1,
由k≠0,可得k=$\frac{2t}{1-{t}^{2}}$(t≠±1,t≠0)②
又联立$\left\{\begin{array}{l}{y=k(x+t)}\\{4{x}^{2}+3{y}^{2}=12}\end{array}\right.$消去y得(4+3k2)x2+6k2tx+3k2t2-12=0,
且△>0恒成立,且x1+x2=-$\frac{6{k}^{2}t}{4+3{k}^{2}}$,x1x2=$\frac{3{k}^{2}{t}^{2}-12}{4+3{k}^{2}}$,
所以y1+y2=k(x1+x2)+2kt=$\frac{8kt}{4+3{k}^{2}}$,所以得P($\frac{-6{k}^{2}t}{λ(4+3{k}^{2})}$,$\frac{8kt}{λ(4+3{k}^{2})}$),
代入①式得$\frac{12{k}^{4}{t}^{2}}{(4+3{k}^{2})^{2}{λ}^{2}}$+$\frac{16{k}^{2}{t}^{2}}{{λ}^{2}(4+3{k}^{2})^{2}}$=1,所以λ2=$\frac{4{k}^{2}{t}^{2}}{4+3{k}^{2}}$,
又将②式代入得,λ2=$\frac{4}{(\frac{1}{{t}^{2}})^{2}+\frac{1}{{t}^{2}}+1}$,t≠0,t≠±1,
易知($\frac{1}{{t}^{2}}$)2+$\frac{1}{{t}^{2}}$+1>1,且($\frac{1}{{t}^{2}}$)2+$\frac{1}{{t}^{2}}$+1≠3,
所以λ2∈(0,$\frac{4}{3}$)∪($\frac{4}{3}$,4),
所以λ的取值范围为{λ|-2<λ<2且λ≠0,且λ≠±$\frac{2\sqrt{3}}{3}$}.
点评 熟练掌握圆锥曲线的定义和性质、向量相等、直线与圆锥曲线的相交问题及根与系数的关系是解题的关键.本题需要较强的计算能力,注意分类讨论的思想方法应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
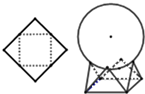 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )| A. | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a、b、c、d中至多有三个是正数 | B. | a、b、c、d中至多有两个是正数 | ||
| C. | a、b、c、d都是正数 | D. | a、b、c、d都是负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com