
分析 根据条件求出直线恒过定点C(1,3),根据面积相等得到直线过AB的中点,求出a的值,结合直线斜率的几何意义进行求解即可.
解答 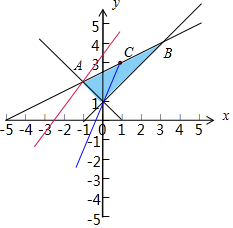 解:由直线ax-y-a+3=0得a(x-1)+(3-y)=0,
解:由直线ax-y-a+3=0得a(x-1)+(3-y)=0,
即直线恒过C(1,3),x,y的不等式组$\left\{\begin{array}{l}{x-2y+5≥0}\\{x+y-1≥0}\\{x-y+1≤0}\end{array}\right.$表示的平面区域如图:由$\left\{\begin{array}{l}{x-2y+5=0}\\{x-y+1=0}\end{array}\right.$解得B(3,4),$\left\{\begin{array}{l}{x+y-1=0}\\{x-2y+5=0}\end{array}\right.$解得A(-1,2),可得C(1,3)是AB的中点,
若直线ax-y-a+3=0将区域分成面积相等的两部分,
直线只需经过顶点(0,1),(0,1)代入ax-y-a+3=0,解得a=2.
z=4x-ay=4x-2y,即y=2x-$\frac{z}{2}$,经过区域内的点B时,目标函数取得最大值.
此时最大值为:4×3-2×4=4.
故答案为:4.
点评 本题主要考查线性规划的应用,直线恒过定点以及三角形面积相等的应用,直线斜率的计算,综合性较强,利用数形结合是解决本题的关键.


科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
已知点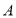 、
、 分别是椭圆
分别是椭圆 :
: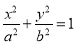 (
( )的上顶点和左焦点,若
)的上顶点和左焦点,若 于圆
于圆 :
: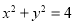 相切于点
相切于点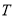 ,且点
,且点 是线段
是线段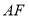 靠近点
靠近点 的三等分点,则椭圆
的三等分点,则椭圆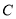 的标准方程为 .
的标准方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
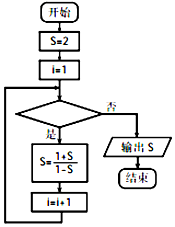 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )| A. | i≤2015? | B. | i≤2016? | C. | i≤2017? | D. | i≤2018? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$) | B. | (0,$\sqrt{3}$) | C. | ($\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知等差数列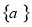 ,
, 为数列
为数列 的前
的前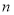 项和,若
项和,若 (
( ),记数列
),记数列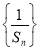 的前
的前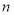 项和为
项和为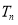 ,则
,则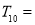 ( )
( )
A.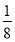 B.
B.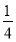
C. D.
D.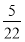
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:选择题
具有性质: 的函数,我们称为满足“倒负”变换的函数,下列函数:
的函数,我们称为满足“倒负”变换的函数,下列函数:
①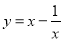 ;②
;② ;③
;③ 其中满足“倒负”变换的函数是( )
其中满足“倒负”变换的函数是( )
A.①② B.①③ C.②③ D.①
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=g(x)的最小正周期为π | |
| B. | 函数y=g(x)的图象的一条对称轴为直线x=$\frac{π}{8}$ | |
| C. | ${∫}_{0}^{\frac{π}{2}}$g(x)dx=$\sqrt{2}$ | |
| D. | 函数y=g(x)在区间[$\frac{π}{12}$,$\frac{5π}{8}$]上单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com