
| A. | (-∞,$\sqrt{3}$) | B. | (0,$\sqrt{3}$) | C. | ($\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
分析 根据题意,由函数的奇偶性与单调性分析可得f(x)在区间[0,+∞)上递减,则f(2${\;}^{lo{g}_{3}a}$)>f(-$\sqrt{2}$)可以转化为2${\;}^{lo{g}_{3}a}$<$\sqrt{2}$,变形可得log3a<$\frac{1}{2}$,解可得a的取值范围,即可得答案.
解答 解:根据题意,f(x)是定义在R上的偶函数,且在区间(-∞,0]上单调递增,
则其在区间[0,+∞)上递减,
f(2${\;}^{lo{g}_{3}a}$)>f(-$\sqrt{2}$)?f(2${\;}^{lo{g}_{3}a}$)>f($\sqrt{2}$)?2${\;}^{lo{g}_{3}a}$<$\sqrt{2}$,
即log3a<$\frac{1}{2}$,
解可得0<a<$\sqrt{3}$;
故选:B.
点评 本题考查函数奇偶性与单调性的综合应用,结合函数奇偶性和单调性之间的关系以及对数的运算性质是解决本题的关键.


科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3},AB=2$,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$,则cosC=$\frac{7}{9}$.则三角形ABC的面积为2$\sqrt{2}$.
如图,在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3},AB=2$,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$,则cosC=$\frac{7}{9}$.则三角形ABC的面积为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费x | 2 | 3 | 4 | 5 | 6 |
| 销售额y | 29 | 41 | 50 | 59 | 71 |
| A. | 101.2 | B. | 108.8 | C. | 111.2 | D. | 118.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
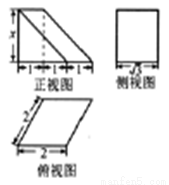
某几何体的三视图如下图所示,且该几何体的体积为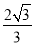 ,则正视图中
,则正视图中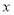 的值为( )
的值为( )
A.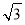 B.
B.
C.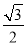 D.
D.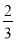
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
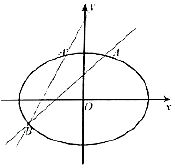 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,直线l:y=kx+1(k≠0)与椭圆E交于A,B两点,当k=1时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,直线l:y=kx+1(k≠0)与椭圆E交于A,B两点,当k=1时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com