
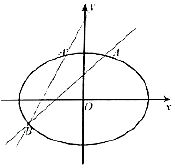
 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,直线l:y=kx+1(k≠0)与椭圆E交于A,B两点,当k=1时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,直线l:y=kx+1(k≠0)与椭圆E交于A,B两点,当k=1时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.分析 (1)利用椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,椭圆E的右焦点(c,0)到直线l:y=x+1的距离为$\sqrt{2}$,
列出方程,求出$a=2,b=\sqrt{3}$,即可得到椭圆E的方程.
(2)设A(x1,y1),B(x2,y2),则有A'(-x1,y1),将y=kx+1代入椭圆方程$\frac{x^2}{4}+\frac{y^2}{3}=1$,利用韦达定理,求出直线A'B的方程为$y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}+{x_1}}}({x+{x_1}})$,通过x=0,得到y值,即可推出A'B恒过y轴上的一个定点.
解答 (普通中学做)解:(1)∵椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,∴$\frac{1}{a^2}+\frac{9}{{4{b^2}}}=1$.…(2分)
∵椭圆E的右焦点(c,0)到直线l:y=x+1的距离为$\sqrt{2}$,
∴$\frac{{|{c+1}|}}{{\sqrt{2}}}=\sqrt{2}$,∴c=1.…(4分)
又a2=b2+c2,解得$a=2,b=\sqrt{3}$,故椭圆E的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(6分)
(2)设A(x1,y1),B(x2,y2),则有A'(-x1,y1),
将y=kx+1代入椭圆方程$\frac{x^2}{4}+\frac{y^2}{3}=1$,得(3+4k2)x2+8kx-8=0.…(8分)
∴${x_1}+{x_2}=-\frac{8k}{{3+4{k^2}}}$,${x_1}{x_2}=-\frac{8}{{3+4{k^2}}}$.…(10分)
直线A'B的方程为$y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}+{x_1}}}({x+{x_1}})$,
令x=0,得$y=\frac{{{x_1}{y_2}+{x_2}{y_1}}}{{{x_2}+{x_1}}}=\frac{{{x_1}({k{x_2}+1})+{x_2}({k{x_1}+1})}}{{{x_2}+{x_1}}}=\frac{{2k{x_1}{x_2}}}{{{x_2}+{x_1}}}+1=\frac{{2k({-\frac{8}{{3+4{k^2}}}})}}{{-\frac{8k}{{3+4{k^2}}}}}+1=3$,
故A'B恒过y轴上的一个定点(0,3).…(12分)
点评 本题考查椭圆方程的求法,直线与椭圆位置关系的综合应用,直线恒过定点,考查转化思想以及计算能力.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$) | B. | (0,$\sqrt{3}$) | C. | ($\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱椎P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD为梯形,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2,DA=PD=$\sqrt{3}$,E为BC的中点,连结AE,交BD于点O.
如图,在四棱椎P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD为梯形,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2,DA=PD=$\sqrt{3}$,E为BC的中点,连结AE,交BD于点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e] | B. | $(1+\frac{1}{e},e]$ | C. | (1,e] | D. | $[1+\frac{1}{e},e]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=g(x)的最小正周期为π | |
| B. | 函数y=g(x)的图象的一条对称轴为直线x=$\frac{π}{8}$ | |
| C. | ${∫}_{0}^{\frac{π}{2}}$g(x)dx=$\sqrt{2}$ | |
| D. | 函数y=g(x)在区间[$\frac{π}{12}$,$\frac{5π}{8}$]上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,PA=$\frac{{2\sqrt{3}}}{3}$a,AD=2a.
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,PA=$\frac{{2\sqrt{3}}}{3}$a,AD=2a.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
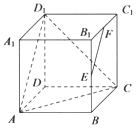 如图,在正方体ABCD-A1B1C1D1中,点E,F分别为BB1,B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别为BB1,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 1+i | D. | -1+i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com