
 如图,在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3},AB=2$,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$,则cosC=$\frac{7}{9}$.则三角形ABC的面积为2$\sqrt{2}$.
如图,在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3},AB=2$,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$,则cosC=$\frac{7}{9}$.则三角形ABC的面积为2$\sqrt{2}$. 分析 在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3}$,由半角公式可得cosB=$\frac{1}{3}$,在△ABC,和ABD,BDC中利用余弦定理关系,求解边长BC和AC.可得cosC和三角形ABC的面积
解答 解:在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3}$,由半角公式可得cosB=$\frac{1}{3}$,
在△ABC中,设BC=a,AC=3b,则由余弦定理可得cos∠ADB=$\frac{4{b}^{2}+\frac{16}{3}-4}{4b×\frac{4\sqrt{3}}{3}}$
cos∠CDB=$\frac{{b}^{2}+\frac{16}{3}-{a}^{2}}{2b×\frac{4\sqrt{3}}{3}}$
∵∠ADB与∠CDB互补,
∴cos∠ADB=-cos∠CDB,
∴$\frac{4{b}^{2}+\frac{16}{3}-4}{4b×\frac{4\sqrt{3}}{3}}$=$\frac{{b}^{2}+\frac{16}{3}-{a}^{2}}{2b×\frac{4\sqrt{3}}{3}}$…①
由cosB=$\frac{1}{3}$=$\frac{4+{a}^{2}-9{b}^{2}}{8a}$…②
由①②解得a=3,b=1,
BC=3,AC=3,
那么cosC=$\frac{B{C}^{2}+A{C}^{2}-A{B}^{2}}{2BC•AC}$=$\frac{18-4}{18}=\frac{7}{9}$.
则sinC=$\frac{4\sqrt{2}}{9}$,
∴三角形ABC的面积为S=$\frac{1}{2}$BC•ACsinC=2$\sqrt{2}$.
故答案为:$\frac{7}{9}$,2$\sqrt{2}$
点评 本题考查三角形中余弦定理的灵活应用,考查转化思想和方程思想,以及化简计算能力.属于中档题.


科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
若数列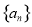 满足
满足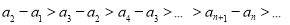 ,则称数列
,则称数列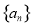 为“差递减”数列.若数列
为“差递减”数列.若数列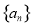 是“差递减”数列,且其通项
是“差递减”数列,且其通项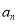 与其前
与其前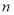 项和
项和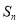 (
( )满足
)满足 (
( ),则实数
),则实数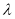 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
已知点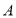 、
、 分别是椭圆
分别是椭圆 :
: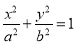 (
( )的上顶点和左焦点,若
)的上顶点和左焦点,若 于圆
于圆 :
: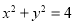 相切于点
相切于点 ,且点
,且点 是线段
是线段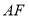 靠近点
靠近点 的三等分点,则椭圆
的三等分点,则椭圆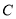 的标准方程为 .
的标准方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$) | B. | (0,$\sqrt{3}$) | C. | ($\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com