
分析 (1)根据绝对值的选项得到f(x)≥2,求出满足条件的x的值即可;
(2)根据绝对值的性质求出x的范围,结合集合的包含关系求出a的范围即可.
解答 解:(1)a=-1时,f(x)=|2x+1|+|2x-1|≥|2x+1-2x+1|=2,
即x=±$\frac{1}{2}$时,“=”成立,
故不等式的解集是{x|x=±$\frac{1}{2}$};
(2)由|2x-a|+|2x-1|≤|2x+1|得:|2x-a|≤|2x+1|-|2x-1|≤|2x+1-2x-1|=2,
故-2≤2x-a≤2,故$\frac{a-2}{2}$≤x≤$\frac{a+2}{2}$,
故[$\frac{1}{2}$,1]⊆[$\frac{a-2}{2}$,$\frac{a+2}{2}$],
故$\left\{\begin{array}{l}{\frac{a-2}{2}≤\frac{1}{2}}\\{\frac{a+2}{2}≥1}\end{array}\right.$,解得:a∈[0,3].
点评 本题考查了绝对值的性质,考查集合的包含关系以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | 6 | D. | $4\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3},AB=2$,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$,则cosC=$\frac{7}{9}$.则三角形ABC的面积为2$\sqrt{2}$.
如图,在△ABC中,$cos\frac{1}{2}∠ABC=\frac{{\sqrt{6}}}{3},AB=2$,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$,则cosC=$\frac{7}{9}$.则三角形ABC的面积为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 堑堵,我国古代数学名词,其三视图如图所示.《九章算术》中有如下问题:“今有堑堵,下广二丈,袤一十八丈六尺,高二丈五尺,问积几何?”意思是说:“今有堑堵,底面宽为2丈,长为18丈6尺,高为2丈5尺,问它的体积是多少?”(注:一丈=十尺).答案是( )
堑堵,我国古代数学名词,其三视图如图所示.《九章算术》中有如下问题:“今有堑堵,下广二丈,袤一十八丈六尺,高二丈五尺,问积几何?”意思是说:“今有堑堵,底面宽为2丈,长为18丈6尺,高为2丈5尺,问它的体积是多少?”(注:一丈=十尺).答案是( )| A. | 25500立方尺 | B. | 34300立方尺 | C. | 46500立方尺 | D. | 48100立方尺 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
某几何体的三视图如下图所示,且该几何体的体积为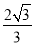 ,则正视图中
,则正视图中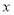 的值为( )
的值为( )
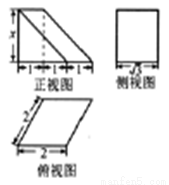
A.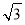 B.
B.
C.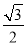 D.
D.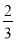
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com