
分析 由已知向量的坐标求得$\overrightarrow{a}$•$\overrightarrow{b}$、|$\overrightarrow{a}$+$\overrightarrow{b}$|的最值,代入f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-|$\overrightarrow{a}$+$\overrightarrow{b}$|,换元后利用配方法求得函数的最值.
解答 解:∵$\overrightarrow{a}$=(cos$\frac{3}{2}$x,sin$\frac{3}{2}$x),$\overrightarrow{b}$=(cos$\frac{x}{2}$,-sin$\frac{x}{2}$),
∴$\overrightarrow{a}•\overrightarrow{b}=cos\frac{3x}{2}cos\frac{x}{2}-sin\frac{3x}{2}sin\frac{x}{2}$=cos2x,
$\overrightarrow{a}+\overrightarrow{b}=(cos\frac{3x}{2}+cos\frac{x}{2},sin\frac{3x}{2}-sin\frac{x}{2})$,
$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{(cos\frac{3x}{2}+cos\frac{x}{2})^{2}+(sin\frac{3x}{2}-sin\frac{x}{2})^{2}}$=$\sqrt{2+2cos2x}=2|cosx|$,
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-|$\overrightarrow{a}$+$\overrightarrow{b}$|=cos2x+2|cosx|,
又x∈[-$\frac{π}{2}$,$\frac{π}{2}$],
∴f(x)=2cos2x+2cosx-1,
令t=cosx(0≤t≤1),
则函数化为y=$2{t}^{2}+2t-1=2(t+\frac{1}{2})^{2}-\frac{3}{2}$,
∴当t=0时,ymin=-1,当t=1时,ymax=3.
∴函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为-1,最大值为3.
点评 本题考查平面向量的数量积运算,考查三角函数中的恒等变换应用,训练了利用换元法和配方法求函数的最值,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{11}{10}$ | C. | $\frac{13}{14}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
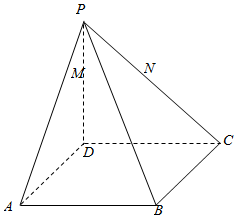 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com