
���� ��1������Բ��������Ϊ$\frac{\sqrt{2}}{2}$���ҽ���ΪF���϶���ΪA���ҡ�AOF�����Ϊ$\frac{1}{2}$��OΪ����ԭ�㣩���г������飬���a=$\sqrt{2}$��b=1���ɴ��������ԲC�ķ��̣�
��2����P��x1��y1����Q��x2��y2����${x}_{1}�ʣ�0��\sqrt{2}��$������OM��OP�����|PF|+|PM|=|QF|+|QM|=$\sqrt{2}$���Ӷ������PFQ���ܳ�Ϊ��ֵ2$\sqrt{2}$��
��� �⣺��1������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0����������Ϊ$\frac{\sqrt{2}}{2}$���ҽ���ΪF���϶���ΪA��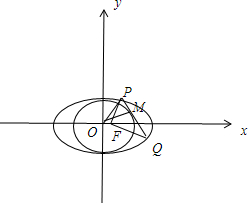
�ҡ�AOF�����Ϊ$\frac{1}{2}$��OΪ����ԭ�㣩��
��$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{2}bc=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����a=$\sqrt{2}$��b=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{2}+{y}^{2}=1$��
��2�����P�ڵ�һ���ޣ���P��x1��y1����Q��x2��y2����${x}_{1}�ʣ�0��\sqrt{2}��$��
��|PF|=$\sqrt{��{x}_{1}-1��^{2}+{{y}_{1}}^{2}}$=$\sqrt{{{x}_{1}}^{2}-2{x}_{1}+1+1-\frac{{{x}_{1}}^{2}}{2}}$
=$\sqrt{\frac{1}{2}{{x}_{1}}^{2}-2{x}_{1}+2}$=$\sqrt{\frac{1}{2}��{x}_{1}-2��^{2}}$=$\frac{\sqrt{2}}{2}��2-{x}_{1}��$��
����OM��OP����|PM|=$\sqrt{|OP{|}^{2}-|OM{|}^{2}}$
=$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}-1}$=$\sqrt{{{x}_{1}}^{2}+1-\frac{{{x}_{1}}^{2}}{2}-1}$=$\frac{\sqrt{2}}{2}{x}_{1}$��
��|PF|+|PM|=$\frac{\sqrt{2}}{2}��2-{x}_{1}��+\frac{\sqrt{2}}{2}{x}_{1}=\sqrt{2}$��
ͬ����|QF|+|QM|=$\sqrt{2}$��
��|PF|+|QF|+|PQ|=|PF|+|QF|+|PM|+|QM|=2$\sqrt{2}$��
���PFQ���ܳ�Ϊ��ֵ2$\sqrt{2}$��
���� ���⿼����Բ���̡���ռ����빫ʽ��ֱ�߷��̵Ȼ���֪ʶ������������֤����������������������黯����ת��˼�롢�����뷽��˼�룬���鴴����ʶ��Ӧ����ʶ�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ԲC��$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$����ΪF��-1��0��������Ϊx=-2��
��֪��ԲC��$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$����ΪF��-1��0��������Ϊx=-2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 81 | B�� | 79 | C�� | 77 | D�� | 75 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | 2 | C�� | $\sqrt{5}$ | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q | B�� | �Vp��q | C�� | p�ĩVq | D�� | ���Vp���ģ��Vq�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com