
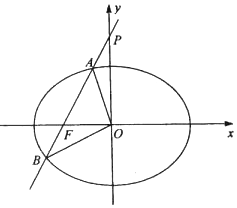
 已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.
已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.分析 (1)由椭圆的左焦点为F(-1,0),左准线为x=-2,列出方程组求出a,b,由此能求出椭圆C的标准方程.
(2)①设直线l的方程为y=k(x+1),则P(0,k),代入椭圆得(1+2k2)x2+4k2x+2k2-2=0,由此利用韦达定理、向量知识,结合已知条件能证明λ+μ为常数-4.
②当直线OA,OB分别与坐标轴重合时,△AOB的面积${S}_{△AOB}=\frac{\sqrt{2}}{2}$,当直线OA,OB的斜率均存在且不为零时,设OA:y=kx,OB:y=-$\frac{1}{k}x$,将y=kx代入椭圆C,得到x2+2k2x2=2,由此利用换元法结合已知条件能求出△AOB的面积的取值范围.
解答 解:(1)∵椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2,
∴由题设知c=1,$\frac{{a}^{2}}{c}$=2,a2=2c,
∴a2=2,b2=a2-c2=1,
∴椭圆C的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
证明:(2)①由题设知直线l的斜率存在,设直线l的方程为y=k(x+1),则P(0,k),
设A(x1,y1),B(x2,y2),直线l代入椭圆得x2+2k2(x+1)2=2,
整理,得(1+2k2)x2+4k2x+2k2-2=0,
∴${x}_{1}+{x}_{2}=\frac{-4{k}^{2}}{1+2{k}^{2}}$,${x}_{1}{x}_{2}=\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
由$\overrightarrow{PA}=λ\overrightarrow{AF}$,$\overrightarrow{PB}=μ\overrightarrow{BF}$,知$λ=\frac{-{x}_{1}}{1+{x}_{1}}$,$μ=\frac{-{x}_{2}}{1+{x}_{2}}$,
∴λ+μ=-$\frac{{x}_{1}+{x}_{2}+2{x}_{1}{x}_{2}}{1+{x}_{1}+{x}_{2}+{x}_{1}{x}_{2}}$=-$\frac{\frac{-4{k}^{2}}{1+2{k}^{2}}+\frac{4{k}^{2}-4}{1+2{k}^{2}}}{1+\frac{-4{k}^{2}}{1+2{k}^{2}}+\frac{2{k}^{2}-2}{1+2{k}^{2}}}$=-$\frac{-4}{-1}=-4$(定值).
∴λ+μ为常数-4.
解:②当直线OA,OB分别与坐标轴重合时,△AOB的面积${S}_{△AOB}=\frac{\sqrt{2}}{2}$,
当直线OA,OB的斜率均存在且不为零时,设OA:y=kx,OB:y=-$\frac{1}{k}x$,
设A(x1,y1),B(x2,y2),将y=kx代入椭圆C,得到x2+2k2x2=2,
∴${{x}_{1}}^{2}=\frac{2}{2{k}^{2}+1}$,${{y}_{1}}^{2}=\frac{2{k}^{2}}{2{k}^{2}+1}$,
同理,${{x}_{2}}^{2}=\frac{2{k}^{2}}{2+{k}^{2}}$,${{y}_{2}}^{2}=\frac{2}{2+{k}^{2}}$,
△AOB的面积S△AOB=$\frac{OA•OB}{2}$=$\sqrt{\frac{({k}^{2}+1)^{2}}{(2{k}^{2}+1)({k}^{2}+2)}}$,
令t=k2+1∈[1,+∞),则S△AOB=$\sqrt{\frac{{t}^{2}}{(2t-1)(t+1)}}$=$\sqrt{\frac{1}{2+\frac{1}{t}-\frac{1}{{t}^{2}}}}$,
令μ=$\frac{1}{t}$∈(0,1),则${S}_{△AOB}=\sqrt{\frac{1}{-{μ}^{2}+μ+2}}$=$\sqrt{\frac{1}{-(μ-\frac{1}{2})^{2}+\frac{9}{4}}}$∈[$\frac{2}{3}$,$\frac{\sqrt{2}}{2}$).
综上所述,△AOB的面积的取值范围是[$\frac{2}{3}$,$\frac{\sqrt{2}}{2}$].
点评 本题考查椭圆方程、韦达定理、向量知识、直线方程等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,函数与方程思想、数形结合思想,考查创新意识、应用意识,是中档题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 愿意被外派 | 不愿意被外派 | 合计 | |
| 70后 | 20 | 20 | 40 |
| 80后 | 40 | 20 | 60 |
| 合计 | 60 | 40 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
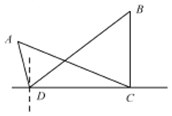 如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )| A. | $20\sqrt{6}$海里 | B. | $40\sqrt{6}$海里 | C. | $20(1+\sqrt{3})$海里 | D. | 40海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com