
分析 (Ⅰ)因为a=1,所以f(x)=|x+1|+|x-1|≥|x+1-x+1|=2,即可求函数f(x)的最小值;
(Ⅱ)因为2∉A,所以f(2)>5,即|a+2|+|a-2|>5,分类讨论,即可求a的取值范围.
解答 解:(Ⅰ)因为a=1,所以f(x)=|x+1|+|x-1|≥|x+1-x+1|=2,
当且仅当(x+1)(x-1)≤0时,即-1≤x≤1时,f(x)的最小值为2.(5分)
(Ⅱ)因为2∉A,所以f(2)>5,即|a+2|+|a-2|>5,(7分)
当a<-2时,不等式可化为-a-2-a+2>5,解得$a<-\frac{5}{2}$,所以$a<-\frac{5}{2}$;
当-2≤a≤2时,不等式可化为a+2-a+2>5,此时无解;
当a>2时,不等式可化为a+2+a-2>5,解得$a>\frac{5}{2}$,所以$a>\frac{5}{2}$;
综上,a的取值范围为$({-∞,-\frac{5}{2}})∪({\frac{5}{2},+∞})$.(10分)
点评 本题考查不等式的解法,考查绝对值不等式的运用,考查分类讨论的数学思想,属于中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{5}{2}$,4] | B. | [$\frac{5}{2}$,$\frac{9}{2}$) | C. | [4,$\frac{9}{2}$) | D. | [4,$\frac{9}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
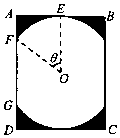 某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.
某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{3}$ | C. | $\frac{11}{3}$ | D. | -1或$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
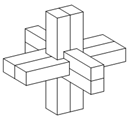 如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )
如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )| A. | $2\sqrt{6}$ | B. | $2\sqrt{7}$ | C. | $4\sqrt{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
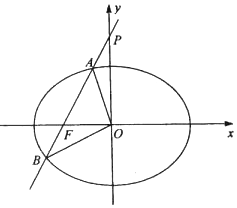 已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.
已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com