
| A. | ①② | B. | ③④ | C. | ②③ | D. | ①④ |
分析 化简函数f(x),求出函数f(x)的值域,判断①正确;
计算f($\frac{π}{8}$)不是函数的最值,判断x=$\frac{π}{8}$不是函数的对称轴,判断②错误;
画出f(x)的图象,根据图象平移判断函数f(x+β)不是奇函数,判断③错误;
根据f(x)=f(x+2α)求出方程在α∈(0,$\frac{3π}{4}$)的解判断④正确.
解答  解:由题意,f(x)=2cos22x-2=cos4x-1;
解:由题意,f(x)=2cos22x-2=cos4x-1;
对于①,cos4x∈[-1,1],∴cos4x-1∈[-2,0],
∴函数f(x)的值域为[-2,0],①正确;
对于②,x=$\frac{π}{8}$时,f($\frac{π}{8}$)=cos$\frac{π}{2}$-1=-1,
∴x=$\frac{π}{8}$不是函数f(x)的一条对称轴,∴②错误;
对于③,∵f(x)=cos4x-1的图象如图所示,;
函数f(x+β)的图象是f(x)的图象向左或向右平移|β|个单位,
它不会是奇函数的,故③错误;
对于④,f(x)=f(x+2α),∴cos4x-1=cos(4x+8α)-1,
∴8α=2kπ,∴α=$\frac{kπ}{4}$,k∈Z;
又α∈(0,$\frac{3π}{4}$),α=$\frac{π}{4}$或$\frac{π}{2}$,④正确.
综上,真命题是①④.
故选:D.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了命题真假的应用问题,是综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
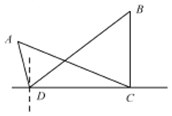 如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )| A. | $20\sqrt{6}$海里 | B. | $40\sqrt{6}$海里 | C. | $20(1+\sqrt{3})$海里 | D. | 40海里 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com