
分析 (Ⅰ)方法一、求出f(x)的解析式和导数,设直线与曲线y=f(x)相切,其切点为(x0,f(x0)),求出切线的方程,代入P的坐标,整理成三次方程,运用两点存在定理,考虑方程的根的情况即可得证;
方法二、求出f(x)的解析式和导数,设直线与曲线y=f(x)相切,其切点为(x0,f(x0)),求出切线的方程,代入P的坐标,整理成三次方程,构造三次函数,求出导数和单调区间及极值,即可得证;
(Ⅱ)由题意可得当x≤0时,e2x(ax2+2x-1)+1≥0,构造$h(x)=a{x^2}+2x-1+\frac{1}{{{e^{2x}}}}$,设$m(x)=ax+1-\frac{1}{{{e^{2x}}}}$,求出导数,讨论a的范围,运用单调性即可得到a的范围.
解答 解法一:(Ⅰ)证明:当a=4时,f(x)=e2x(4x2+2x-1),
f'(x)=e2x•2(4x2+2x-1)+e2x(8x+2)=2e2x(4x2+6x)…(1分)
设直线与曲线y=f(x)相切,其切点为(x0,f(x0)),
则曲线y=f(x)在点(x0,f(x0))处的切线方程为:y-f(x0)=f'(x0)(x-x0),
因为切线过点P(1,0),所以-f(x0)=f'(x0)(1-x0),…(2分)
即$-{e^{2{x_0}}}({4{x_0}^2+2{x_0}-1})=2{e^{2{x_0}}}({4{x_0}^2+6{x_0}})({1-{x_0}})$,
∵${e^{2{x_0}}}>0$,∴$8{x_0}^3-14{x_0}+1=0$,…(3分)
设g(x)=8x3-14x+1,
∵g(-2)=-35<0,g(0)=1>0,g(1)=-5<0,g(2)=37>0…(4分)
∴g(x)=0在三个区间(-2,0),(0,1),(1,2)上至少各有一个根.
又因为一元三次方程至多有三个根,所以方程8x3-14x+1=0恰有三个根,
故过点P(1,0)有三条直线与曲线y=f(x)相切. …(5分)
(Ⅱ)∵当x≤0时,f(x)+1≥0,即当x≤0时,e2x(ax2+2x-1)+1≥0,
∴当x≤0时,$a{x^2}+2x-1+\frac{1}{{{e^{2x}}}}≥0$,…(6分)
设$h(x)=a{x^2}+2x-1+\frac{1}{{{e^{2x}}}}$,
则$h'(x)=2ax+2-\frac{2}{{{e^{2x}}}}=2(ax+1-\frac{1}{{{e^{2x}}}})$,…(7分)
设$m(x)=ax+1-\frac{1}{{{e^{2x}}}}$,则$m'(x)=a+\frac{2}{{{e^{2x}}}}$.
(1)当a≥-2时,∵x≤0,∴$\frac{2}{{{e^{2x}}}}≥2$,从而m'(x)≥0(当且仅当x=0时,等号成立)
∴$m(x)=ax+1-\frac{1}{{{e^{2x}}}}$在(-∞,0]上单调递增,
又∵m(0)=0,∴当x≤0时,m(x)≤0,从而当x≤0时,h'(x)≤0,
∴$h(x)=a{x^2}+2x-1+\frac{1}{{{e^{2x}}}}$在(-∞,0]上单调递减,又∵h(0)=0,
从而当x≤0时,h(x)≥0,即$a{x^2}+2x-1+\frac{1}{{{e^{2x}}}}≥0$
于是当x≤0时,f(x)+1≥0,…(9分)
(2)当a<-2时,令m'(x)=0,得$a+\frac{2}{{{e^{2x}}}}=0$,∴$x=\frac{1}{2}ln({-\frac{2}{a}})<0$,
故当$x∈(\frac{1}{2}ln(-\frac{2}{a}),\left.0]$时,$m'(x)=\frac{a}{{{e^{2x}}}}({{e^{2x}}+\frac{2}{a}})<0$,
∴$m(x)=ax+1-\frac{1}{{{e^{2x}}}}$在$(\frac{1}{2}ln(-\frac{2}{a}),\left.0]$上单调递减,
又∵m(0)=0,∴当$x∈(\frac{1}{2}ln(-\frac{2}{a}),\left.0]$时,m(x)≥0,
从而当$x∈(\frac{1}{2}ln(-\frac{2}{a}),\left.0]$时,h'(x)≥0,
∴$h(x)=a{x^2}+2x-1+\frac{1}{{{e^{2x}}}}$在$(\frac{1}{2}ln(-\frac{2}{a}),\left.0]$上单调递增,
又∵h(0)=0,
从而当$x∈(\frac{1}{2}ln(-\frac{2}{a}),0)$时,h(x)<0,即$a{x^2}+2x-1+\frac{1}{{{e^{2x}}}}<0$
于是当$x∈(\frac{1}{2}ln(-\frac{2}{a}),0)$时,f(x)+1<0,…(11分)
综合得a的取值范围为[-2,+∞).…(12分)
解法二:(Ⅰ)当a=4时,f(x)=e2x(4x2+2x-1),
f'(x)=e2x•2(4x2+2x-1)+e2x(8x+2)=2e2x(4x2+6x),…(1分)
设直线与曲线y=f(x)相切,其切点为(x0,f(x0)),
则曲线y=f(x)在点(x0,f(x0))处的切线方程为y-f(x0)=f'(x0)(x-x0),
因为切线过点P(1,0),所以-f(x0)=f'(x0)(1-x0),…(2分)
即$-{e^{2{x_0}}}({4{x_0}^2+2{x_0}-1})=2{e^{2{x_0}}}({4{x_0}^2+6{x_0}})({1-{x_0}})$,
∵${e^{2{x_0}}}>0$,∴$8{x_0}^3-14{x_0}+1=0$…(3分)
设g(x)=8x3-14x+1,则g'(x)=24x2-14,令g'(x)=0得$x=±\sqrt{\frac{7}{12}}$,
当x变化时,g(x),g'(x)变化情况如下表:
| x | $(-∞,-\sqrt{\frac{7}{12}})$ | $-\sqrt{\frac{7}{12}}$ | $(-\sqrt{\frac{7}{12}},\sqrt{\frac{7}{12}})$ | $\sqrt{\frac{7}{12}}$ | $(\sqrt{\frac{7}{12}},+∞)$ |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 极大值$\frac{28}{3}\sqrt{\frac{7}{12}}+1$ | ↘ | 极小值$-\frac{28}{3}\sqrt{\frac{7}{12}}+1$ | ↗ |
点评 本题考查导数的运用:求切线的方程和单调区间和极值,考查分类讨论思想方法和构造函数法,化简整理的运算能力,属于难题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
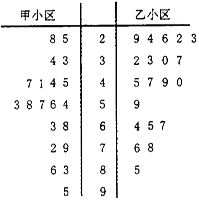 某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:| 甲小区(有健康广场) | 乙小区(无健康广场) | 合计 | |
| 身体综合素质良好 | 350 | 300 | 650 |
| 身体综合素质一般 | 650 | 700 | 1350 |
| 合计 | 1000 | 1000 | 2000 |
| P(K2>k) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 1.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{5}{2}$,4] | B. | [$\frac{5}{2}$,$\frac{9}{2}$) | C. | [4,$\frac{9}{2}$) | D. | [4,$\frac{9}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{9}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
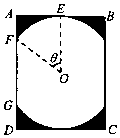 某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.
某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{3}$ | C. | $\frac{11}{3}$ | D. | -1或$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②③ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com