
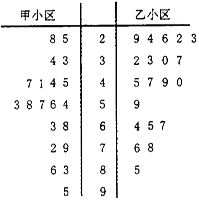
 ij��Ϊ���˽�ȫ�����˶���չ��Ч����ѡ��ס����������Ƶ�С�����Աȣ�һ��ǰ�ڼ�С������������Ʊ�������˽����㳡��һ���ֱ�����С�����ü���������ķ�����ȡ20����Ϊ���������������ۺ����ʲ��ԣ����Ե÷ַ����ľ�Ҷͼ������ʮλΪ��������ΪҶ����ͼ��
ij��Ϊ���˽�ȫ�����˶���չ��Ч����ѡ��ס����������Ƶ�С�����Աȣ�һ��ǰ�ڼ�С������������Ʊ�������˽����㳡��һ���ֱ�����С�����ü���������ķ�����ȡ20����Ϊ���������������ۺ����ʲ��ԣ����Ե÷ַ����ľ�Ҷͼ������ʮλΪ��������ΪҶ����ͼ��| ��С�����н����㳡�� | ��С���������㳡�� | �ϼ� | |
| �����ۺ��������� | 350 | 300 | 650 |
| �����ۺ�����һ�� | 650 | 700 | 1350 |
| �ϼ� | 1000 | 1000 | 2000 |
| P��K2��k�� | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 1.706 | 3.841 | 5.024 | 6.635 | 7.879 |
���� ��1�����þ�Ҷͼ���ɵü�С������С������λ����
��2���г������������k�����ٽ�ֵ�Ƚϣ����ɵó����ۣ�
��� �⣺��1�������⣬��С������λ��Ϊ55����С������λ��Ϊ42.5��
��2��2��2��������
| ��С�����н����㳡�� | ��С���������㳡�� | �ϼ� | |
| �����ۺ��������� | 350 | 300 | 650 |
| �����ۺ�����һ�� | 650 | 700 | 1350 |
| �ϼ� | 1000 | 1000 | 2000 |
���� ���⿼�龥Ҷͼ����������Լ���֪ʶ�����ã�����ѧ���ļ��������������е��⣮


 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 21 | B�� | -21 | C�� | 441 | D�� | -441 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com