
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)根据函数的单调性求出f(x)的最大值和最小值,问题转化为m>2eln3+1-$\frac{3e}{a}$,令g(a)=2eln3+1-$\frac{3e}{a}$,(a∈(e,+∞)),根据函数的单调性求出m的范围即可.
解答 解:(1)∵f′(x)=alnx+a+b,
∴f′(1)=a+b=0,故b=-a,
∴f(x)=axlnx-ax,且f′(x)=alnx,
当a>0时,x∈(0,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0,
∴f(x)在(0,1)递减,在(1,+∞)递增;
a<0时,x∈(0,1)时,f′(x)>0,x∈(1,+∞)时,f′(x)<0,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(2)∵a∈(e,+∞),
∴f(x)在(0,1)递减,在(1,+∞)递增,
又f($\frac{1}{3}$e)=$\frac{1}{3}$aeln$\frac{1}{3}$<0,f(1)=-a,f(3e)=3aeln3>0,
∴x∈[$\frac{1}{3}$e,3e]时,f(x)max=f(3e)=3aeln3,f(x)min=f(1)=-a,
∴若对任意x1,x2∈[$\frac{1}{3}$e,3e]都有|f(x1)-f(x2)|<(m+eln3)a+3e成立,
只需(m+eln3)a+3e>f(3e)-f(1)=3aeln3+a,
即m>2eln3+1-$\frac{3e}{a}$,
令g(a)=2eln3+1-$\frac{3e}{a}$,(a∈(e,+∞)),
易知g(a)>g(e)=2eln3-2,
∵存在a∈(e,+∞),使得m>2eln3+1-$\frac{3e}{a}$成立,
∴m>2eln3-2,
故实数m的范围是(2eln3-2,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54种 | B. | 72种 | C. | 120种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
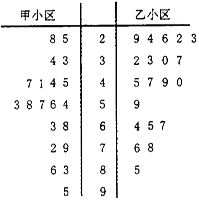 某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:| 甲小区(有健康广场) | 乙小区(无健康广场) | 合计 | |
| 身体综合素质良好 | 350 | 300 | 650 |
| 身体综合素质一般 | 650 | 700 | 1350 |
| 合计 | 1000 | 1000 | 2000 |
| P(K2>k) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 1.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $-\frac{1}{2}$ | C. | 5 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com